Задача о назначении

      При рассмотрении транспортных задач можно было заметить, что ТЗ иногда оказывается вырожденной. Это происходит, если при некотором допустимом распределении поставка в любую клетку, кроме последней, удовлетворяет спрос всего столбца, используя при этом все ресурсы соответствующей строки.

      В рассматриваемой задаче каждый ресурс назначается только на одну работу, а каждая работа требует только одного ресурса. Следовательно, задача о назначении есть полностью вырожденная форма транспортной задачи. В этом случае методы решения транспортных задач оказываются малоэффективными: при любом назначении всегда автоматически совпадают поставки по строке со спросом по столбцу и, поэтому, вместо  получаем  ненулевых значений  и, в связи с этим, необходимо заполнить матрицу  величинами  и совершать «фиктивные перевозки».

      Специальный метод решения задачи о назначении основан на следующих теоремах.

Теорема 1. Если  минимизирует  по всем  таким, что  минимизирует также функционал

 

Доказательство:

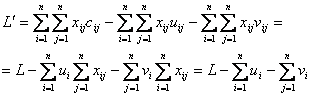
т.е. решение не изменится, если прибавить к любому столбцу или строке матрицы  некоторую константу или вычесть ее из них.

Теорема 2. Если все  и можно отыскать набор , такой, что , то это решение оптимально, т.е. .

Доказательство. (самостоятельно)

      Рассматриваемый метод решения сводится к прибавлению констант к строкам и столбцам и вычитанию их из строк и столбцов до тех пор, пока достаточное число величин  не обращается в нуль, что дает искомое решение.

      В 1912 году венгерский математик Кёниг (König D.) среди других утверждений доказал теорему, благодаря которой оказалось возможным построить алгоритм решения задач о назначении.

      Пусть дана  матрица , некоторые элементы которой являются нулями, а другие произвольны. Обозначим через  - совокупность всех  строк, а через  - совокупность всех  столбцов. Множество рядов матрицы (т.е. множество ее строк и столбцов) называется опорным, если удаление этих рядов приводит к исчезновению из нее всех нулей. Если минимальное опорное множество состоит из  строк и  столбцов, то можно утверждать, что .

      Минимальное число рядов в опорном множестве матрицы  назовем индексом рассредоточения –.

       В качестве примера рассмотрим матрицу .

 

 

      Как , так и  являются опорными множествами, причем меньше из них состоит из четырех рядов . Можно найти опорное множество, состоящее из еще меньшего числа рядов.  Для матрицы  оказывается  и .

      Совокупность нулей матрицы образует связку  строк и  столбцов, если эти  нулей стоят на пересечении  различных строк и  различных столбцов. Так, обведенные рамкой нули образуют связку

.

      Каждая строка и каждый столбец встречаются в этом выражении ровно по одному разу.

Максимальной связкой называют ту связку, которая содержит наибольшее число нулей. Это число называют индексом квадратности матрицы - .

      Теорема Кёнига формулируется следующим образом:

,

т.е. минимальное число опорного множества равно максимальному числу нулей связки, или            индекс рассредоточения матрицы равен индексу ее квадратности.

 

      Для поиска максимальной связки можно предложить следующий алгоритм:

 

В строке или столбце, который содержит наименьшее число нулей, обведем один из нулей, а затем вычеркнем все нули, которые находятся в той же строке или в том же столбце, что и обведенный квадратной рамкой нуль.

Повторить пункт 1, пока существуют непомеченные нули.

 

Алгоритм поиска минимального опорного множества:

 

пометить звездочкой (*) все строки, которые не содержат ни одного обведенного квадратной рамкой нуля;

пометить звездочкой столбец, содержащий перечеркнутый нуль, хотя бы в одной из помеченных строк;

пометить звездочкой строку, содержащую обведенный нуль, хотя бы в одном из помеченных столбцов;

повторять пункты 2 и 3, пока не останется строк или столбцов, которые ещё можно пометить;

перечеркнуть каждую непомеченную строку и каждый помеченный столбец.

 

Алгоритм решения задачи о назначении.

 

В каждом столбце таблицы выберем наименьший элемент и вычтем его из всех элементов этого столбца.

.

Описанный прием позволяет получить хотя бы один нуль в каждом столбце.

В каждой строке таблицы выберем наименьший элемент и вычтем его из всех элементов этой строки:

.

Найти максимальную связку и определить индекс квадратности матрицы.

Если индекс квадратности , решение найдено

Найти минимальное опорное множество.

Из всех непрочеркнутых элементов выбрать наименьшее число.

Вычесть это число из всех непрочеркнутых элементов и прибавить его ко всем дважды прочеркнутым элементам.

Перейти к пункту 3.

 

Пример. Для неоднородной сети ЭВМ перераспределить вычислительные ресурсы, если известны потери, связанные с функционированием -го ресурса в -ом узле.

 

C1 С2 С3 С4 С5 L1 26 14 1 1 13 L2 23 17 4 0 10 L3 15 15 12 12 0 L4 0 0 11 25 15 L5 17 3 0 14 24

 

 

 

 

 

 

 

 

 

 

 

 

 

.

.

Обведем , обведем квадратной рамкой элемент  и вычеркнем ;

Обведем  и вычеркнем ;

Обведем  и вычеркнем .

Индекс квадратности .

Пометим , далее , далее . Прочеркнем  и получим опорное множество.

Минимальный непрочеркнутый элемент .

      7.

 

 

 

 

 

 

 

 

 

 

 

Остальные элементы не изменяются .

Обведем ; обведем , вычеркнем .

Обведем , вычеркнем .

Обведем , вычеркнем .

Обведем .

=18+10+11+9+19=67.

Индекс квадратности - .

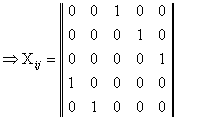
      Аналогичный расчет позволяет определить максимальные потери, которые составляют 167 ед. Между наилучшим и наихудшим решением имеется разница 100 ед. и существует ещё 118 промежуточных решений.