Задача о максимальном потоке
Теорема Форда-Фалкерсона (1962)

(Ford L. R. I., Fulkerson D.R.)

Рассмотрим некоторый произвольный ориентированный граф. Будем рассматривать его как сеть труб, по которым некоторое вещество движется от истока (где оно производится с некоторой постоянной скоростью) к стоку (где оно потребляется - с той же скоростью). Очевидно, что вместо потоков вещества можно совершенно аналогично рассматривать движение тока по проводам, деталей по конвейеру, информации по линиям связи или товаров от производителя к потребителю.

Как и в задаче о кратчайших путях, каждую дугу графа мы помечаем некоторым числом. Но если раньше это число означало длину или стоимость пути, то теперь это скорее ширина дороги, или пропускная способность трубы – максимальное количество вещества, которое может быть перенесено потоком в этой трубе за единицу времени. Например, она может быть 200 литров в час, или 20 ампер (если речь идёт об электричестве).

Мы считаем, что в вершинах вещество не накапливается - сколько прихо­дит, столько и уходит (если вершина не является истоком или стоком). Это свойство называется «законом сохранения потока» (flow conservation). Для элек­трического тока это свойство называется первым правилом Кирхгофа (Kirchhoff's Current Law).

Задача о максимальном потоке для данной сети состоит в следующем: найти максимально возможную скорость производства (и потребления) вещества, при которой его ещё можно доставить от истока к стоку при данных пропуск­ных способностях труб.

Потоки в сетях

В этом разделе мы дадим точное определение сетей и потоков в них, обсу­дим их свойства, сформулируем задачу о максимальном потоке и введём неко­торые полезные обозначения.

Сети и потоки

Назовем сетью ориентированный граф G = (V,E), каждой дуге (u,v) Î Е которого поставлено в соответствие число с(u,v) ³ 0, называе­мое пропускной способностью данной дуги. В случае (u,v) Ï Е мы полагаем с(u,v) = 0. В графе мы будем выделять две особые вершины: исток (source) s и сток (sink) t. Для простоты мы предполагаем, что в графе нет «бесполезных» вершин, то есть каждая вершина v Î V лежит на каком-то пути s-…-v-…-t из истока в сток. В этом случае граф связен и |Е| ³ |V| - 1.

Дадим теперь определение потока в вышеописанной сети. Пусть дана некоторая сеть G = (V,E), пропускная способность которой задаётся матрицей с. Пусть рассматриваемая сеть имеет исток s и сток t. Потоком (flow) в сети G назовём функцию f: V х V ® R, обладающую следующими тремя свойствами.

Ограничение, связанное с пропускной способностью (capacity constraint):

f(u,v) £ c(u, v) для всех u,v из V.

Кососимметричность (skew symmetry):

f(u,v) = -f(v,u) для всех u,v из V.

Сохранение потока (flow conservation):

 для всех u из V - {s,t}.

Очевидно, что величина f(u, v) может быть как положительной, так и отрицательной. Она определяет, сколько вещества движется из вершины u в вершину v. В этом случае отрица­тельные значения соответствуют движению в обратную сторону.

Величина потока f определяется как следующая сумма:

     (1)

В соответствии с данной формулой мы складываем потоки по всем рёбрам, выходящим из истока. Величина потока обозначается F или |f|. Задача о максимальном потоке (maximum-flow problem) состоит в следующем: для данной сети G с истоком s и стоком t найти поток максимальной величины.

Вернемся к трем нашим свойствам потока в сети. Первое из приведенных свойств – ограничения, связанной с пропускной способностью – означает, что поток из од­ной вершины в другую не превышает пропускной способности дуги. Второе – кососомметричность – представляет собой соглашение о том, что отрицательные числа соответствуют потоку в обратном направлении. Из него следует также, что f(u,u) = 0 для любой вершины u (положим v = u). Третье свойство – сохранение потока – означает, что для любой верши­ны u (кроме стока и истока) сумма потоков во все другие вершины равна нулю. Учитывая кососимметричность, это свойство можно переписать так:

(теперь переменная суммирования обозначена и) и интерпретировать следующим образом: сумма всех потоков из других вершин в данную равна нулю.

Заметим также, что если вершины u и v не соединены дугой, то поток между ними, т.е. f(u,v), равен нулю. Действительно, если (u,v) Ï Е и (v,u) Ï Е, то с(u, v) = c(v, u) = 0. Тогда из первого свойства следует, что f(u, v) £ 0 и f(v, u) £ 0. Учитывая тот факт, что f(u,v) = -f(v,u), мы приходим к выводу, что f(u, v) = f(v, u) = 0.

Разделим суммарный поток, поступающий в данную вершину v и суммарный поток, из неё выходящий (т.е. положительные и отрицательные значения f(u,v)). Тогда сумму

    (2)

назовём входящим (в вершину v) потоком. Выходящий поток определяется аналогично:

     (3)

Теперь закон сохранения потока можно сформулировать так: для любой вершины, кроме истока и стока, входящий поток равен исходящему потоку.

Рассмотрим простой пример. Пусть некоторое издательство занимается печатью журнала «Мир полиграфии» на типографии в Москве (исток s) и складирует их в Самаре (сток t). Она арендует место в грузовиках фирмы-перевозчика, и место это ограничено: из города u в город v можно доставить не более с(u, v) журналов в день. Задача состоит в том, чтобы перевозить максимально возможное количество журналов из Москвы в Самару. При этом путь может занимать несколько дней, и журналы могут ждать отправки в промежуточных пунктах, но необходимо, чтобы для каждо­го пункта число ежедневно прибывающих журналов было равно числу увозимых (иначе журналов не хватит или они будут накапливаться). Тем самым выполнено свойство сохранения потока. Величиной потока будет число журналов, отгружаемых из Москвы. Нас же интересует поток максимальной величины.

Пусть задан некоторый поток, в соответствии с которым, из вершины u в вер­шину v в день отправляется f(u,v) журналов; если f(u,v) равно 0, журналы не отправляются; отрицательные значения f(u,v) соответствуют журналам, прибы­вающим в u из v.

Очевидно, что реальная ситуация не впол­не описывается нашей моделью. А именно, наша модель не учитывает встречные перевозки. Если из вершины v в вершину u ежедневно везут восемьсот журналов, а из u в v ежедневно везут триста журналов, то чему должны быть равны f(v,u) и f(u,v)? Напомним, что в соответствии с нашими предыдущими рассуждениями эти величины должны быть противоположны. Мы полагаем f(v,u) = 800 – 300 = 500, a f(u,v) = 300 – 800 = 500. Те же значения функции f соответству­ют ежедневным перевозкам пятисот журналов из вершины v в вершину u, так что в нашей модели встречные перевозки автоматически сокращаются. Впрочем, и в реальности встречные перевозки разумно «сократить» друг с другом, при этом места на грузовиках понадобится только меньше. Тем самым автоматически сократятся затраты на перевозку.

Таким образом, в наших дальнейших рассуждениях мы можем исключить встречные перевозки, не меняя задачи по существу.

Сети с несколькими истоками и стоками

Можно рассматривать задачу о максимальном потоке для случая несколь­ких истоков и стоков. Например, издательство из предыдущего примера, может иметь m типографий {,,…,} и n складов {,,…,}. Это обстоятельство не усложняет дела, потому что такой вариант проблемы можно свести к ранее рассмотренному. Можно построить эквивалентную сеть с одним истоком и одним стоком. Для этого следует добавить общий исток (supersource) s, из которого вести дуги с бесконечной пропуск­ной способности во все прежние истоки. Аналогичным образом из всех прежних стоков необходимо провести дуги в общий сток (supersink) t. Легко видеть, что каждый поток в сети эквивалентной сети соответствует потоку в исходной сети и наоборот.

Закон сохранения потока

В процессе дальнейших рассуждений мы будем использовать следующее соглашение: если в выражении на месте вершины стоит множество вершин, то имеется в виду сумма по всем элементам этого множества. Это относится и к случаю нескольких переменных. Например, если Х и Y – множества вершин, то

В этих обозначениях закон сохранения потока запишется как f(u,V) = 0 для всех u Î V \ {s,t}.

Приведём несколько полезных свойств таких неявных сумм

Лемма 1. Пусть f – поток в сети G = (V,E). Тогда для любого Х Í V выполнено

f(X,X) = 0.

Для любых X, Y Í V выполнено

f(X,Y) = –f(Y,X).

Для любых X, Y, Z Í V из Х Ç Y = Æ следует

f(XÈY,Z) = f{X,Z) + f(Y,Z)

и

f{Z,XÈY) = f(Z,X) + f(Z,Y).

Для примера докажем с использованием таких обозначений, что величина потока равна сумме потоков из всех вершин в сток:

F = f(V,t).    (4)

Интуитивно это ясно, но можно провести и фор­мальное рассуждение. По определению,

F = f(s,V).

Применяя лемму 1, имеем

f(s,V) = f(V,V) – f(V\{s},V) = f(V,V\{s}) = f(V,t) + f(V,V\{s,t}).

По закону сохранения потока второе слагаемое равно 0, и остаётся f(V,t).

Метод Форда-Фалкерсона

В этом разделе мы рассмотрим метод Форда-Фалкерсона отыскания мак­симального потока в сети с ограниченными пропускными способностями. Мы говорим о методе, а не об алгоритме, поскольку есть несколько алгоритмов, реализующих этот метод. Ниже будет приведена один из этих алгоритмов. Ключевую роль в методе Форда-Фалкерсона играют три понятия: остаточные сети, дополняю­щие пути и сечения.

Поиск максимального потока методом Форда-Фалкерсона проводится по шагам. Вначале поток нулевой (и величина его равна нулю). На каждом шаге мы увеличиваем значение потока. Для этого мы находим «дополняющий путь», по которому можно пропустить дополнительный поток, и используем его для увеличения суммарного потока. Этот шаг повторяется, пока есть дополняющие пути. Как покажет теорема о максимальном потоке и минимальном сечении, рассмотренная ниже, полученный поток будет максимальным.

Остаточные сети

Пусть дана сеть и поток в ней. Тогда остаточная сеть – это сеть,  состоящая из тех дуг, поток по которым можно увеличить. Строгое определение остаточной сети таково:

Пусть G = (V,E) – некоторая сеть с истоком s и стоком t. Пусть f  поток в этой сети. Для любой пары вершин u и v рассмотрим остаточную пропускную способность из u в v, определяемую как

     (5)

Остаточная пропускная способность определяет, сколько ещё потока можно направить из вершины u в вершину v. Например, если c(u,v) = 16, a f(u, v) = 11, то мы можем переслать ещё  = 5 единиц по дуге (u,v). Следует заметить, что остаточная пропускная способность  может превосходить пропускную способность c(u,v), если в данный момент поток f(u,v) отрицателен. Например, если c(u,v) = 16, a f(u,v) = –4, то  = 20. В самом деле, мы можем увеличить поток на 4, отменив встречный поток, и ещё отправить 16 единиц, не превышая пропускной способности рассматриваемой дуги (u,v).

Сеть , где

,

назовём остаточной сетью сети G, порождённой потоком f. Её дуги, называемые остаточными дугами, допускают по­ложительный поток.

Обратим внимание на то, что остаточная дуга (u,v) не обязана быть дугой сети G. Ины­ми словами, может оказаться, что выражение  не является верным. Такая дуга из u в v появляется, когда f(u,v) < 0, т.е. когда имеется некоторый поток в обратном направлении. Таким образом, если дуга (u,v) принадлежит остаточной сети, то хотя бы одна из дуг (u,v) и (v,u) было в исходной сети. Тогда получаем следующую оценку:

Пропускную способность дуги остаточной сети  мы полагаем рав­ной величине . Следующая лемма показывает соотношение потоков в исходной и в остаточной сетях.

Лемма 2. Пусть G = (V, Е) – сеть с истоком s и стоком t, a f – поток в ней. Пусть – остаточная сеть сети G, порождённая потоком f. Пусть j – поток в . Тогда сумма f + j, определённая как

(f + j)(u,v) = f(u,v) + j(u,v),

является по­током в сети G величины |f + j| = |f| + |j|.

 

Доказательство. Сначала докажем, что f + j будет потоком. Проверим косо­симметричность. Для всех u, v Î V выполнено:

(f + j)(u, v) = f(u, v) + j (u, v) = -f(v, u) - j (v, u) =

= -(f(v, и) + j(v, и)) = -(f + j)(v, и).

Проверим условие, связанное с ограниченной пропускной способностью. За­метим, что j (u,v) £ (u,v) для всех u,v Î V, поэтому:

(f + j)(u, v) = f(u, v) + j (u, v) £ f(u, v) + (c(u, v) – f(u, v)) = c(u, v).

Проверим закон сохранения потока. Для всех u Î V \ {s,t} выполнено ра­венство:

(f + j)(u, V) = f(u, V) + j(u, V) = 0 + 0 = 0.

И, наконец, найдём величину суммарного потока:

|f + j| = (f + j)(s, V) = f(s, V) + j (s, V) = |f| + |j|.

Дополняющие пути

Пусть f – поток в сети G = (V,E). Назовём дополняющим путём  простой путь из истока s в сток t в остаточной сети . Из опре­деления остаточной сети вытекает, что по всем дугам (u,v) дополняющего пути можно переслать ещё некоторый дополнительный поток, не превысив их пропускную способность.

Величину наи­большего потока, который можно переслать по дополняющему пути р, назовём остаточной пропускной способностью пути р:

Рассмотрим следующую лемму:

Лемма 3. Пусть f - поток в сети G = (V, Е), а p - дополняющий путь в . Определим функцию : V х V ® R следующим образом:

      (6)

Тогда  - поток в сети  и  .

Теперь видно, что если добавить поток  к потоку f, получится поток в сети G с большим значением. Сформуем следствие из только что рассмотренной леммы.

Следствие 1. Пусть f - поток в сети G=(V,E), а р - дополняющий путь в сети . Рассмотрим поток , заданный равенством (6). Тогда функция

является потоком в сети G величины

Доказательство. Данное утверждение вытекает из лемм 2 и 3.

Сечения в сетях

Метод Форда-Фалкерсона добавляет последовательно потоки по дополня­ющим путям, пока не получится максимальный поток. Как мы вскоре увидим (теорема о максимальном потоке и минимальном сечении), величина потока максимальна в том и только в том случае, когда остаточная сеть не содержит дополняющих путей. Для доказательства нам понадобится понятие сечения сети.

Назовём сечением сети G = (V,E) разбиение множества V на две части S и Т = V \ S, для которых s Î S и t Î Т. Пропускной способностью сечения (S,T) называют сумму с(S, Т) пропускных способностей пересекающих разрез рёбер. Кроме то­го, для заданного потока f величина потока через сечение (S, T) определяется как сумма f(S,T) по пересекающим сечение дугам. Ми­нимальным сечением называется сечение наименьшей пропускной способности (среди всех сечений данной сети).

Очевидно, что поток через сечение, в отличие от пропускной способности сечения может включать и отрицательные слагаемые.

Следующая лемма утверждает, что величины потоков через все сечения одинаковы (и равны величине потока).

Лемма 4. Пусть f - поток в сети G с истоком s и стоком t, a (S, Т) – сечение  сети G. Тогда поток f(S,T) через сечение (S,T) равен |f|.

Доказательство. Многократно используя лемму 1, получаем

f(S,T) = f(S,V) – f(S,S) = f(S,V) = f(s,V) + f(S \ s,V) = f(s,V) = |f|

Доказанное выше равенство (3) (величина потока равна потоку в сток) немедленно следует из этой леммы.

Следствие 2. Величина любого потока f в сети G не превосходит пропускной способности любого сечения сети G.

Доказательство. Пусть (S,T) – произвольное сечение сети G. В силу леммы 4 и ограничений на потоки по дугам, имеем:

Сформулируем теперь и докажем основную теорему данного раздела.

Теорема 1 (о максимальном потоке и минимальном сечении).

Пусть f - по­ток в сети G = (V,E). Тогда следующие утверждения равносильны:

1. Поток f максимален (является потоком максимальной величины) в сети G.

2. Остаточная сеть  не содержит дополняющих путей.

3. Для некоторого сечения (S,T) сети G выполнено равенство |f|=c(S,T). В этом случае, как показывает следствие 2, разрез является минимальным, то есть имеет минимально возможную пропускную способность.

Доказательство.

Из (1) следует (2): Рассуждая от противного, допустим, что поток f максимален, но  содержит дополняющий путь р. Рассмотрим сумму f + , где  задаётся равенством (6). В соответствии со следствием 1 эта сумма является потоком в G, величина которого больше |f|, что противоречит максимальности f.

Из (2) следует (3): Пусть в сети  нет пути из истока s в сток t. Рассмотрим множество

S = {v Î V : в  существует путь из s в v}.

Положим Т = V \ S. Очевидно, что s Î S, а t Î T, так как в  нет пути из s в t. Поэтому пара (S, Т) – сечение. Ни для каких u Î S и v Î Т дуга (u, v) не принадлежит  (в противном случае вершина v попала бы в S). Поэтому, f(u, v) = c(u,v). Исходя из леммs 4, |f| = f(S,T) = c(S,T).

Из (3) следует (1): Для любого сечения (S,Т) в соответствии со следствием 2 выполнено |f| £ c(S.T). Поэтому из равенства |f| = c(S, Т) следует, что поток f максимален.

Общая схема алгоритма Форда-Фалкерсона

Пусть задано исходное распределение потоков по дугам графа, отображающего топологическую структуру сети, а также пропускные способности дуг. Необходимо найти максимально возможное для данной сети значение суммарного потока между источником и адресатом.

     Согласно теореме о максимальном потоке и минимальном сечении максимально возможное значение суммарного потока равно пропускной способности минимального сечения между источником и адресатом.

     Примем следующие обозначения (часть из них уже использовалась нами при описании метода Форда-Фалкерсона):

c (x, y) – пропускная способность дуги x, y;

f_i (x, y) – поток, приписанный дуге x, y , на i-том шаге алгоритма;

E – множество ребер сети;

s – узел-источник сети;

t – узел-адресат сети;

x, y – промежуточные узлы сети.

     Алгоритм применим для любого допустимого потока, например, пусть .

1.    Пометить узел s символом (+).

2.    Если существует непомеченный узел, в который ведет ненасыщенная дуга, то есть y: , иначе перейти к пункту 5.

3.    Если y = t, направить по найденному маршруту s – t дополнительный поток

 

и перейти к пункту 1.

4.    Если y ≠ t, выполнить пункт 2.

5.    Если не существует дуги c (x, y) > f (x, y), выбрать не помеченный узел y: , пометить узел y символом  (–) и выполнить пункт 2.

6.    Если для любой помеченной вершины справедливо, что все смежные вершины пометить нельзя, значить найден максимальный поток.

     Β – множество помеченных вершин, – дополнение Β.

 

     Пример 1. Найти максимальный поток и минимальное сечение для графа, пропускная способность каждого ребра равна 1.

 

 

 

 

 

 

 

 

 

 

 

Сетевая модель задачи о максимальном потоке

     3 – минимальное сечение

     3 – максимальный поток

 

 

     Решение.

1.    Пусть исходный поток будет нулевой: .

 

 

 

 

2.      Пометим ребра 01, 13, 36 знаком + и направим по найденному маршруту поток 1.

 

	Маршрут для потока f1(x, y)

 

 

 

 

 

 

 

 

 

3.      Пометим ребра 03, 35, 56 знаком (+) и направим по найденному маршруту поток 1.

 

 

 

 

 

 

	Маршрут для потока f2(x, y)

 

 

Полученный поток f₂ (x, y) содержит по крайней мере одну насыщенную дугу – то есть является "полным" потоком.

4.    Попробуем улучшить полученный поток:

1.    Пометим знаком (+) узел 0.

2.    Пометим знаком (+) ненасыщенные дуги  04 и 45. Так как из вершин 5 выходит насыщенная дуга 56, пометим знаком (-) ненулевой поток 35. Так как из вершины 3 выходит насыщенная дуга 36, пометим знаком (-) ненулевой дуги 13. Пометим знаком (+) ненасыщенные дуги 12, 26.

3.    На вновь открытом маршруте +0.4+4.5-3.5-1.3+1.2+2.6 вычислим приращение "полного" потока равен 1.

4.    Пометим ребро 05 символом (+), так как из вершины 5 выходит насыщенная дуга 56, пометим знаком (–) ненулевой поток 45. То есть все узлы сети можно разбить на два непересекающихся множества

Β = {0,4,5} и Β= {1,2,3,6}.

 

     Пример 2. Заданы топология и пропускные способности каналов замкнутой информационной сети. Найти минимальное сечение и максимальный поток для пары источник-адресат.

s = 0, t = 6.

 

     Решение:

	Сетевая модель задачи о  максимальном потоке (пример 2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

      1)

1.    Пусть исходный поток будет нулевой

     .

     Пометим узел s знаком (+).

2.    Пометим ребра 01, 13, 36, а, следовательно, узлы 0, 1, 3, 6 знаком (+).

3.    Направим по найденному маршруту поток интенсивностью:

     .

	Маршрут для потока f1(x, y)

 

 

 

 

 

 

 

 

 

 

2) 

1.      Пометим знаком (+) узел 0.

2.      Пометим ребра 03, 35, 56, а, следовательно, узлы 0, 3, 5, 6 знаком (+) и направим по маршруту поток интенсивностью

Полученный поток f₂(x, y) содержит по крайней мере одну насыщенную дугу на любом маршруте из 0 в 6, то есть является «полным» потоком. Интенсивность найденного суммарного потока равна 5.

3)   Попробуем улучшить этот поток.

1.                                                                                                                Пометим знаком (+) узел 0.

2.                                                                                                                Пометим знаком (+) ненасыщенные дуги 04 и 45. Так как из вершины 5 выходит насыщенная дуга 56, пометим знаком (–) ненулевой поток 35 (узел 3). Так как из вершины 3 выходит насыщенная дуга 36, пометим знаком (–) ненулевой поток 13 (узел 1). Пометим знаком (+) ненасыщенные дуги 12 и 26 (узлы 2 и 6).

3.                                                                                                                На вновь открытом маршруте +0,4 +4,5 –3,5 –1,3 +1,2 +2,6 вычислим приращение "полного" потока:

                   

                   Интенсивность суммарного потока равна 7.4)

1.    Пометим знаком(+) узел 0.

	Частичное решение задачи о максимальном потоке (пример 2)

 

 

 

 

 

 

 

 

 

 

 

 

 

2.                                                                                                                Пометим ребро 03 (узел 3) символом (+). Так как из вершины 3 выходит насыщенный поток 36, пометим не нулевой поток 13 (узел 1) знаком (–). Пометим знаком (+) ненасыщенные дуги 12 и 26 (узлы 2 и 6).

3.                                                                                                                На вновь открытом маршруте +0,3 –1,3 +1,2 +2,6 вычислим приращение «полного» потока.

 Интенсивность полного потока равна 8.

5)   Пометим знаком (+) узел 0. Пометим ребро 05 (узел 5) символом (+). Так как из вершины 5 выходит насыщенная дуга 56, пометим знаком (–) ненулевой поток 45 (узел 4) и т.д. Получается, что ни одну вершину пометить нельзя. Следовательно, найденный поток является максимальным.

 

 

 

 

 

 

 

 

 

 

 

 

 

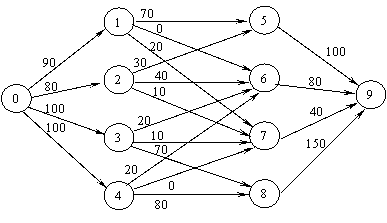
     Пример 3. Заданы топология и пропускные способности каналов замкнутой информационной сети. Найти минимальное сечение и максимальный поток для пары источник-адресат.

s = 0, t = 9.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

     Решение: Пусть исходный поток будет нулевой:

.

1.    Составим таблицу, каждая строка которой помечена парой  и пропускной способностью этой дуги c(x, y). Cтолбцы будут содержать потоком f(x, y), приписанные этому ребру.

2.      Рассматривая всевозможные пути и выделяя маршруты, содержащие по крайней мере одну насыщенную дугу, получаем «полный» поток.

                                                                                 Таблица 1.

 

                                        Продолжение таблицы 1.

 

1 итерация.

f₁(x, y):  +0,1  + 1,5  +5,9

f₂(x, y):  +0,1  + 1,7  +7,9

f₃(x, y):  +0,2  + 2,5  +5,9

и так далее получим «полный» поток , то есть поток, который в любом маршруте 0 – 9 имеет хотя бы одну насыщенную дугу:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.    Попробуем улучшить полученный поток.

1.    Пометим узел 0 знаком (+).

2.    Пометим знаком (+) ненасыщенные дуги 01 и 16. Так как из вершины 6 выходит насыщенная дуга 69, пометим знаком (–) ненулевой поток 36 и знаком (+) ненасыщенные дуги 37 и 79. (y = 9 = t).

+0,1 +1,6 -3,6 +3,7 +7,9

На размеченном маршруте 0 – 9 вычислим приращение «полного» потока:

.

 

 

 

 

 

 

 

 

 

 

 

 

3.      Пометим последовательность ребер +0,1 +1,6 –4,6 +4,7 +7,9. На вновь открытом маршруте 0 – 9 вычислим приращение "полного" потока:

.

 

 

 

 

 

 

 

 

 

 

4.    Окончательно находим, что существует возможность пометить ребра +0,2 +2,5 –1,5 –0,1. Следовательно, все узлы сети можно разбить на два непересекающихся подмножества:

Β = {0,1,2,5} - множество помеченных узлов;

 = {3,4,6,7,8,9} – дополнение множества Β.

      Это и есть один из минимальных разрезов сети, через который может пройти поток не более