Задача упорядочивания
 Алгоритм Джонсона

Каждый из n независимых процессов обработки информации состоит из двух операций, которые последовательно требуют ресурсы А и В на время A_i и B_i соответственно.

Выбрать такой порядок следования процессов, при котором будет обеспечено наименьшее время процесса обработки.

 

          Рассмотрим пример:

i	1	2	3
Ai	30	20	10
Bi	10	20	30

 

          Составим диаграмму Ганта. Данная диаграмма позволяет подсчитать общее время простоя.

 

 

 

 

 

 

 

 

 

 

 

 

          Время простоя – 40 мин.

 

          Обозначим:

          T- полное время процесса обработки,

          X_i- время ожидания ресурсом B i-го процесса.

И так как  не зависит от порядка обработки массивов, то надлежит выбрать такой порядок, при котором

 

 

 

 

 

 

 

 

из рисунка видно:

 

          Теперь исследуем сумму  .

 

 

 

 

 

 

 

 

 

i,r	1	2	3
Ai	30	20	10
Bi	10	20	30
	30	50	60
	-	10	30
	30	40	30

 

Как и следовало ожидать, время простоя = 40 мин.

 

 

 

          Рассмотрим искомый порядок

 

 

и порядок, полученный транспонированием пары (k,k+1)

 

 

          Значения и , получаемые для порядков S₁ и S₂ одинаковы при всех r, кроме, может быть, r=k и r=k+1.

 

          Так, как необходимо найти

         

 

          Это условие выполняется в двух случаях:

 

          а)

 

 

 

 

т.е. если в таблице времен можно найти время A_k , не превосходящее всех прочих времен, то искомый порядок должен начинаться с процесса p_k.

 

          б)

 

 

 

т.е. , если в таблице времен можно найти время B_k+1, меньшее всех прочих времен, то искомый порядок должен завершаться процессом p_k+1.

 

          Таким образом алгоритм можно записать в следующем виде: если таблица времен пуста, решение найдено, иначе

 

Выбирается наименьшее время в таблице времен.

Если это значение относится к операции A принимается решение начать обработку с этого процесса, иначе завершают обработку этим процессом.

Рассмотренный процесс вычеркивается из таблицы времен и переходят к пункту 1.

 

          Пример: Каждый из 8-ми независимых процессов обработки информации состоит из двух операций, которые последовательно требуют ресурсы А и В на время А_i и В_i соответственно. Выбрать такой порядок следования процессов, при котором будет обеспечено наименьшее время процесса обработки.

 

 

          Решение данной задачи приведено в таблице 2.

Таблица 2

количество процессов: 8
имя процесса	1	2.	3.	4.	5.	6.	7.	8.
время А	12	10	14	18	25	20	15	12
время В	10	8	11	12	20	25	20	15
имя процесса	1.	2.	3.	4.	5.	6.	7.	8.
время А	12	10	14	18	25	20	15	12
время В	10	8	11	12	20	25	20	15
время простоя 38
транспозиция пары 2. 8. позиции 2 8
имя процесса	1.	8.	3.	4.	5.	6.	7.	2.
время А	12	12	14	18	25	20	15	10
время В	10	15	11	12	20	25	20	8
время простоя 33
транспозиция пары 1. 7. позиции 1 7
имя процесса	7.	8.	3.	4.	5.	6.	1.	2.
время А	15	12	14	18	25	20	12	10
время В	20	15	11	12	20	25	10	8
время простоя 26
транспозиция пары 3. 6. позиции 3 6
имя процесса	7.	8.	6.	4.	5.	3.	1.	2.
время А	15	12	20	18	25	14	12	10
время В	20	15	25	12	20	11	10	8
время простоя 18
транспозиция пары 8. 7. позиции 2 1
имя процесса	8.	7.	6.	4.	5.	3.	1.	2.
время А	12	15	20	18	25	14	12	10
время В	15	20	25	12	20	11	10	8
время простоя 18
транспозиция пары 4. 5. позиции 4 5
имя процесса	8.	7.	6.	5.	4.	3.	1.	2.
время А	12	15	20	25	18	14	12	10
время В	15	20	25	20	12	11	10	8
время простоя 13
сохранена позиция 2 процесс 7. сохранена позиция 3 процесс 6.

 

 

Обобщение на трехэтапные работы

Алгоритм Джонсона применим для последовательности и процессов, подлежащих выполнению в порядке: A, B, C в двух нижеследующих случаях:

 или .

Тогда осуществляется поиск оптимальных сроков по суммам: A_i+B_i и B_i+C_i .

 

          Пример. Пусть операции над массивами p₁…p₅ заданы сроками выполнения A_i, B_i, C_i (табл. 5). Условие  выполняется. Таким образом имеем таблицу 6.

 

 

          Алгоритм Джонсона позволяет выбрать

 

  или

Модель Раймонда

Каждый из двух независимых процессов обработки информации n=2 состоит из трех операций m=3, которые последовательно монополизируют ресурсы A,B и C, на время A_i, B_i и C_i соответственно.

Выбрать такой порядок следования процессов при котором будет обеспечено наименьшее время обработки.

 

 

Описанный ниже метод применим и для общего случая (n>2, m>3).Рассматриваемую обработку можно представить в следующем виде.

 

 

 

 

 

 

 

 

 

 

 

 

 

Вершины графа

a,b,c,d,e - означают начало соответствующего процесса,

a',b',c',d',e' - завершение процесса,

g - завершение обработки информации.

 

          Моменты времени, которые соответствуют этим вершинам обозначим: t_a, t_b,…

 

          Таким образом задача выбора порядков следования процессов может быть записана в следующем виде:

                                                   (1)

 

                                 (2)

                                      (3)

                                      (4)

 

          Ограничения (3) и (4) отражают тот факт, что один ресурс в одно и тоже время может быть резервирован только одним процессом. Эти ограничения из-за наличия функции неравнозначности вносят нелинейность в рассматриваемую задачу. Заменим ограничения (3) и (4) системой линейных ограничений.

 

          Положим для ресурса A

y₁=0, если длина дуги ba равна 10, ,     

          процесс 1 предшествует процессу 2;

y₁=1, если длина дуги ab равна 2, ,
          процесс 1 следует за процессом 2.

          Введем постоянную M такую, чтобы заведомо выполнялось условие M>t_g. Пусть M=20. Условие (3) можно заменить системой 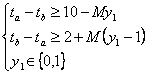(5).

 

                                                (5)

 

          Докажем, что (5) эквивалентно (3):

 

y₁=0,  совпадает с 1 ограничением из (3),

          выполняется всегда;

 

y₁=1,  выполняется всегда,

           совпадает со 2 ограничением из (3).

          Проведя аналогичные рассуждения для ресурса В, получаем:

         

                                               (6)

          В итоге рассматриваемая задача примет вид (1), (2), (5) и (6).

 

 

Методы оптимального размещения
информации на внешних носителях

Оптимальное распределение информации
 на внешнем носителе

 

Пусть задано множество файлов

каждый из которых характеризуется физической длиной L_i и вероятностью обращения p_i, т.е. .

В случае применения ленты, физической длинной файла является длинна того отрезка магнитного носителя, который занимает этот файл (с учетом головного и хвостового битов, а также межблочных промежутков).

В случае применения диска, физической длинной файла считается количество смежных цилиндров, которое ему отведено.

Позиционирование стационарной считывающей головки на начало нужного файла может производиться двумя различными способами:

установка носителя в исходное начальное положение, а затем перемещение в прямом направлении до начала нужного файла,

перемещение носителя кратчайшим путем в прямом или обратном направлении до начала нужного файла.

Поиск информации через начало носителя

         Процесс обращения к нужному файлу можно расчленить на две части:

подвод читающей головки от начала ленты до начала файла и просмотр самого файла;

возврат головки в исходное состояние.

 

                             В обоих случаях длина прогона носителя равна:

.

    Математическое ожидание длины прогона носителя можно записать в виде:

 

,

и в качестве функционала на множестве всех перестановок из m объектов выберем

Найдем необходимые условия оптимальной перестановки G^*. Пусть G^* искомый порядок, а G – порядок, полученный транспозицией пары (j, j+1). Значения F(G^*)  и F(G) различаются может быть слагаемыми  и , т.е.

 

 

Таким образом необходимым условием оптимальной перестановки G^* является:

 или , где

                        Пример. Имеем последовательность шести массивов

 

i	1	2	3	4	5	6
Li	6	4	50	30	9	1
pi	0.13	0.07	0.4	0.1	0.2	0.1
	46	57	125	300	45	10

 

 

 

 

i	6	5	1	2	3	4
Li	1	9	6	4	50	30
pi	0.1	0.2	0.13	0.07	0.4	0.1
	10	45	46	57	125	300

 

          После сортировки по возрастанию  имеем

Зависимость для оптимальной перестановки  в случае поиска информации через начало носителя

i

 

Поиск информации по кратчайшему маршруту

Вероятность последовательного обращения от массива f_i к f_j  равна p_ip_j.

          Длина прогона носителя от f_i к f_j  в этом случае можно записать в виде:

 

fi

fj

fj

fi

          Математическое ожидание длины прогона носителя  представим в виде таблицы на пересечении i строки и  j столбца которой стоит величина .

 

 

 

          В общем случае за целевую функцию возьмем

 

 

          Найдем необходимые условия оптимальной перестановки G^*. Пусть G^* – искомый порядок, а G – порядок, полученный транспозицией пары (j, j+1). Значения F(G^*) и F(G) различаются может быть слагаемыми для k=j и k=j+1.

 

 

          Т.к.

 

 

Это и есть необходимое условие, которое выполнено в двух случаях:

 

, что характерно для начала перестановки G^*.

 

 

 

 

 

 

 

, что характерно для конца перестановки G^*.

 

 

 

     

 

 

 

Рассмотрим алгоритм, по которому практически можно осуществить процесс оптимизации.

 

Массивы сортируются таким образом, чтобы характеристика  не убывала от центра к периферии.

Переменной f присвоить значение адреса массива с наименьшим значением . Вычислить S=f - 1.

Если S < 1, выполнить пункт 8.

Вычислить S1=S+1.

Если условие транспозиции не выполняется, т.е. , выполнить пункт 8.

Выполнить транспозицию пары (S, S1).

Вычислить S=S - 1, перейти к пункту 3.

Если (число массивов), окончить вычисление.

Вычислить f1=f+1.

Если , окончить вычисление.

Выполнить транспозицию пары (f, f1).

Вычислить S = f - 1, f = f1, выполнить пункт 3.

 

          Рассмотрим пример:

          Имеется последовательность шести массивов (j – номер i массива в текущей перестановке)

 

j	1	2	3	4	5	6
i	1	2	3	4	5	6
Li	6	4	50	30	9	1
pi	0.13	0.07	0.4	0.1	0.2	0.1
gi	46	57	125	300	45	10

 

          Вычислить значение целевой функции F(S) для исходной перестановки.

 

 

Массивы сортируем таким образом, чтобы характеристика  убывала от периферии к центру.

 

j	1	2	3	4	5	6
i	3	1	6	5	2	4
li	125	46	10	45	57	300
pi	0.4	0.13	0.1	0.2	0.07	0.1

 

F(S)=2.62

 

f=3, S=2.

S не меньше 1, следовательно выполняем пункт 4.

S1=3.

Рассматриваем пару (S, S1) т.е. (2, 3):

l₂=46, l₃=10,

a₁=0.4, b₄=0.37,

.

Выполним транспозицию пары (2, 3):

 

j	1	2	3	4	5	6
i	3	6	1	5	2	4
li	125	10	46	45	57	300
pi	0.4	0.1	0.13	0.2	0.07	0.1

 

F(S)=2.606

 

S=1, S не меньше 1, S1=2.

Рассматриваем пару (1, 2)

l₁=120, l₃=10,

a₀=0, b₃=0.5,

.

Условие транспозиции не выполняется.

f меньше 6, f1=4.

Рассматриваем пару (3, 4):

l₃=46, l₄=45,

a₂=0.5, b₅=0.17.

Выполним транспозицию пары (3, 4):

 

j	1	2	3	4	5	6
i	3	6	5	1	2	4
li	125	10	45	46	57	300
pi	0.4	0.1	0.2	0.13	0.07	0.1

 

F(S) = 2.596.

 

S = 2 = f -1,  f = f1 = 4.

S не меньше 1, следовательно выполнить пункт 4.

Рассмотрим пару (S, S+1) т.е. (2, 3):

l₃=46, l₄=45,

a₂=0.5,  b₅=0.17,

.

Транспозиция нецелесообразна, выполним пункт 8.

f=4 < m, следовательно f1=5.

Рассмотрим пару (f, f1) т.е. (4, 5):

l₃=46,  l₄=57,

a₂=0.7, b₅=0.1.

Транспозиция нецелесообразна.

Окончить вычисление.

Оптимальная перестановка: 3, 6, 5, 1, 2, 4.

Зависимость для оптимальной перестановки в случае поиска информации по кратчайшему маршруту

 

 

Решение задачи линейного программирования с булевыми переменными
 методом частичного перебора

Предположим, что рассматриваемая модель имеет следующий вид:

,

,

.

Если учитывать лишь условие 3, то существует 2^m возможных решений (x₁, x₂, … x_m) = R. Разумеется многие из них недопустимы из-за ограничений 2.

Рассмотрим некоторое подмножество переменных {x_j}, в котором каждому переменному поставлено в соответствие определенное числовое значение (0 или 1). Такое подмножество называют частичным решением.

Переменные, принадлежащие частичному решению, называют базисными переменными.

Переменные, не входящие в частичное решение, носят название свободных переменных.

Любой конкретный выбор числовых значений свободных переменных называется дополнением соответствующего частичного решения.

Если частичное решение содержит s переменных, то существует 2^m-s дополнений.

Допустим, что известна нижняя оценка оптимального значения целевой функции – b₀ и зафиксировано R – допустимое решение, дающее эту оценку. Если каким-либо образом можно показать, что не существует допустимого дополнения или существующее дополнение не позволяет улучшить текущую нижнюю оценку – b₀, то говорят, что частичное решение d_n, содержащее s переменных, прозондировано, т.е. неявным образом просмотрены 2^m-s дополнений.

Существует тесная связь между основной идеей рассматриваемого метода и принципом оптимальности динамического программирования. Соответствующую формулировку указанного принципа применительно к рассматриваемому алгоритму можно выразить следующим образом: при заданном частичном решении значения остальных переменных должны выбираться так, чтобы дополнение этого решения было оптимальным.

Рассмотрим способ, устанавливающий факт существования допустимого дополнения, дающего значение целевой функции, улучшающее текущую нижнюю оценку – b₀.

 

          Пример 1.

          Если задача содержит ограничение

,

то для частичного решения

не существует допустимого дополнения, т.к. сумма отрицательных коэффициентов при свободных переменных больше разности свободного члена и суммы произведений коэффициентов базисных переменных на значение этих переменных:

т.е., даже полагая x₅ = 1, а x₂ = 0, невозможно выполнить это ограничение.

 

      Смысл рассмотренного примера заключается в следующем:

при заданном частичном решении представим линейные ограничения в виде:

,

где S_n – множество индексов, которыми помечены свободные переменные,

          В_n – множество индексов, которыми помечены базисные переменные.

          Допустимого дополнения не существует, если

.

          Сумма в левой части этого неравенства представляет собой сумму всех отрицательных коэффициентов при свободных переменных. Если эта сумма больше правой части, то, даже полагая x_j = 1, для каждой свободной переменной, где a_ij < 0, невозможно выполнить i-тое ограничение.

Другим важным моментом является то, что при заданном частичном решении иногда удается определить, какое значение должна иметь свободная переменная при любом допустимом дополнении.

 

          Пример 2.

          Если задача содержит ограничение

,

 то для частичного решения

в любом дополнении должно выполняться условие x₃ = 0, т.к. только в этом случае справедливо

.

Этот пример позволяет сделать вывод, что для любой свободной переменной x_k в случае, когда

      Таким образом алгоритм можно написать так:

Обозначим           

Cond Ps –условие допустимости зондируемого решения,

CondPs = TRUE, если "i: FSN_i < FBN_i.

Cond Wi – возможность расширения зондируемого решения,

condWi = TRUE, если

,

в этом случае

Cond Cm – условие полноты зондируемого решения.

d_n = PROBE – зондируемое решение.

DECIS – условие существования решения.

R – решение.

F_min – значение целевой функции.

n = NUMPR – номер зондируемого решения.

 

Вычислить DECIS = FALSE, F_min = 10, n = 1.

Вычислить FSN, FBN, CondPs, CondCm.

Если зондируемое решение недопустимо (CondPs = FALSE), то перейти к пункту 11.

Если допустимое зондируемое решение полно (CondCm = TRUE), перейти к пункту 10.

Вычислить возможность расширения зондируемого решения (CondWi).

Если CondWi = FALSE, выполнить пункт 9.

Расширить зондируемое решение

 

Перейти к пункту 2.

Выполнить искусственное расширение, т.е. вычислить:

d_n = d_n È x_k = 0;  d_n+1 = d_n È x_k = 1;  n = n + 1,

и перейти к пункту 2.

Вычислить R = d_n, F_min = b₀, DECIS = TRUE.

Вычислить n = n – 1, т.е. перейти к зондированию следующего частичного решения.

Если список зондируемых решений не пуст, т.е. n > 0, перейти к пункту 2, иначе окончить вычисления.

 

Для иллюстрации предложенного алгоритма рассмотрим пример:

max F =   3x₁ + 6x₂ + 3x₃ + 6x₄ + 13x₅

- 3x₁ - 6x₂ + 6x₃ + 12x₄ + 7x₅    £  8

6x₁ + 12x₂ - 3x₃ - 6x₄ + 7x₅     £  8

DECIS = FALSE, F_max = –¥, n = 1.

Допустимое решение существует так как:

CondPs = True

("_i: FSN_i < FBN_i)

CondCm = False

 

CondWi : $ i : FSN_i + ïa_ikï > FBN_i;

такого i не существует ÞCondWi = FALSE,

следовательно выполняем 9.

Выполняем искусственное расширение

d₁ = (x₁ x₂ x₃ x₄ 0),  d₂ = (x₁ x₂ x₃ x₄ 1)

n = 2.  S₁ = {1, 2, 3, 4};  B₁ = {5};  S₂ = {1, 2, 3, 4};  B₂ = {5}

CondPs = True

(Зондируемое решение допустимо)

CondCm = False

 

 

CondWi = TRUE: $ i = 2: FSN₂ + ½a₂₂½ > FBN₂, k = 2.

Следовательно, частичное решение можно расширить. Выполняем пункт 7.

Расширяем зондируемое решение

k = 2

S₂ = {1, 3, 4},  B₂ = {2, 5},  d₂ = (x₁ 0 x₃ x₄ 1)

          2.

CondWi = TRUE : $ i = 1: FSN₁ + ½a₁₃½ > FBN₁, k = 3_.

Следовательно, зондируемое решение можно расширить

0	FSN	1	3	4	FBN	CondPs = True (следовательно, зондируемое решение допустимо) CondCm = False (следовательно, зондируемое решение не полно)
0	–12	–3	–3	–6	13
1	–3	–3	6	12	1
2	–9	6	–3	–6	1

x₃ = 0,  S₂ = {1, 4},  B₂ = {2, 3, 5},  d₂ = (x₁ 0 0 x₄ 1).

 

CondWi = TRUE : $ i = 1: FSN₁ + ½a₁₄½ > FBN_1, k = 4,

x₄ = 0,  S₂ = {1},  B₂ = {2, 3, 4, 5},  d₂ = (x₁ 0 0 0 1)

 

 

F_min = 13, R = (0, 0, 0, 0, 1),  DECIS = TRUE,

 

 

 

 

 

 

 

 

 

 

 

n = 0, список задач пуст

F_max = 13,   R = (0, 0, 0, 0, 1)

DECIS = TRUE

          Прекращаем дальнейшие вычисления. Оптимальное значение целевой функции равно 13.

Выбор подпрограмм из заданного набора

При выборе набора подпрограмм, реализующих все необходимые операции над вводимыми в систему данными, во многих случаях необходимо удовлетворять ряду противоречивых требований: увеличению точности определения выходных значений, уменьшению объема памяти, занятого подпрограммами, реализующими алгоритмы управления и информационного поиска, уменьшению времени выполнения подпрограмм.

 

          Рассмотрим следующие задачи.

 

1. Выбор набора логических подпрограмм:

а) минимизирующего объем занимаемой памяти при ограничениях на время   выполнения подпрограмм.

б) минимизирующего время выполнения подпрограмм при ограничениях на объем занимаемой ими памяти.

 

          1.а)

          Пусть задано L подпрограмм, с помощью которых можно полностью реализовать алгоритм системы.

          Номер подпрограммы обозначим через

          Система (алгоритм) состоит из M операций. Номер операции обозначим через

          Каждой подпрограмме припишем коэффициент определяемый по правилу:

 

и переменную, определяемую по правилу:

          Разница между изаключается в том,

что - задается заранее, а

       - находится в результате решения.

          Задача состоит в том, чтобы выбрать набор подпрограмм, реализующий заданные операции за время, не превосходящее  и занимающий минимальный объем памяти - S.

          Таким образом необходимо минимизировать

, где      (1)

S_l - объем памяти занимаемой l-й подпрограммой.

 

                                        (2)

 

          Условие (2) введено для того, чтобы показать, что каждая применяемая подпрограмма должна записываться в З.У. только один раз, независимо от числа операций, в которых она используется.

          Для реализации m-ой операции может быть использована одна и только одна подпрограмма:

 

      (4)

 

          Так как время выполнения операций ограничено:

 

, где (5)

 

- время выполнения l-ой подпрограммы при реализации m-операции,

- число выполнения m-ой операции.

          Формализованная запись исходной задачи содержит линейную целевую функцию (1), линейные ограничения (4) и (5).

          Система ограничений (2) представляет собой нелинейную систему ограничений.

          Можно показать, что любое нелинейное ограничение (2) эквивалентно системе линейных ограничений (3).

 (3)

Таблица 1.

0	0	1	1	1	1	0	0
0	1	0	0	1	0	-1	-1
0	2	0	0	1	0	-2	-2
0	m	0	0	1	0	-m	-m
0	M	0	0	1	0	-M	-M
1	0	0	0	0	1	1	M
1	1	1	1	1	1	0	M-1
1	2	1	1	1	1	-1	M-2
1	m	1	1	1	1	1-m	M-m
1	M	1	1	1	1	1-M	M-M

 

Таким образом, исходная задача сведена к минимизации целевой функции (1) при ограничениях (3), (4), (5).

В рассмотренном случае мы предполагали, что характеристики подпрограмм не зависят от характера входных и выходных данных. В тех случаях, когда это не так, необходимо различать операции обработки данных разного типа. Заметим также, что при выборе набора подпрограмм мы учитываем только длину подпрограммы. Характеристики используемых ее рабочих и информационных массивов не рассматриваются, или, что тоже самое, считается, что длинна каждой подпрограммы указана с учетом используемых объемом памяти для рабочих массивов.

          1.б) В случае необходимости минимизации времени работы системы логических программ целевая функция принимает вид

 

     (6)

 

а вместо ограничения (5) записываем ограничение

 

  (7)

 

          Теперь задача сведена к минимизации целевой функции (6) при ограничениях (3), (4), (7).

 

      Пример 1.

          Задано множество процедур (подпрограмм) L={1,2,3}, реализующие алгоритм, состоящий из 3 ( M=3 ) операций. Известно, что S_l- объем памяти занимаемой l-той процедурой:

t_lm- время реализации l-той процедурой m-ой операции:

 

 

 

      Выбрать набор процедур, реализующих алгоритм за наименьшее время и занимающих объем памяти не превышающий 3 ед.

 

   целевая функция (6)

 

    огр. (7)

 

   огр. (3)

 

    огр. (4)

 

          Решая полученную задачу линейного программирования с булевыми переменными (например методом частичного перебора) получим значение целевой функции F=13 и вектор- решения R=(011110), разворачивая который получим матрицу значений переменных и решение задачи в целом.

 

 

          Таким образом, проведя аналогичный анализ различных t можно придти к выводу:

 

Исходные данные к задаче выбора состава пакета из заданного набора процедур

          Количество операций:   3

          Количество процедур:    3

          Общий ресурс не выше: 3.0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример 2.

Задано множество подпрограмм L = {1, 2, 3, 4}, реализующих алгоритм, состоящий из 3 операций. Известно, что S_l – объем памяти, занимаемый l-ой подпрограммой:

S₁ = 1;  S₂ = 2;  S₃ = 3;  S₄ = 4.

t_lm – время реализации l-ой подпрограммы при выполнении m-ой операции.

t₂₁ = t₃₂ = t₄₃ = 1;  t₁₁ = 2;  t₂₂ = 4;  t₃₃ = 5.

Выбрать набор подпрограмм, реализующих данный алгоритм и занимающий наименьший объем памяти так, чтобы время работы алгоритма не превышало 3 ед. времени.

 

подпрограммы (l)

 

1. N = 1 S₁ = {1,2,3,4,5,6,7}; B₁ = Æ; d₁ = (x₁,x₂,x₃,x₄,x₅,x₆,x₇)

B₀ = 0

 

 

 

 

2. A – не выполняется à $ решение

3. S₁={1,3,4,5,6,7}; B₁={2}; d₁ = (x₁,0,x₃,x₄,x₅,x₆,x₇)

    N=2 S₂={1,3,4,5,6,7}; B₂={2}; d₂ = (x,1,x₃,x₄,x₅,x₆,x₇)

N>0

 

 

6. А – не выполняется à $ `d₂

8. S₂ = Æ

10. B выполняетсяà 0 + [a₉₇ = 4] > 0

11. S₂ = {1,3,4,5,6}; B₂ = {2,7}; d₂ = (x,1,0,x₃,x₄,x₅,x₆,0)

 

 

6. А – не выполняется à $ `d₂

8. S₂ ¹ Æ

10. B выполняетсяà 0 + [a₉₆ = 3] > 0 à x₆ = 0

S₂ = {1,3,4,5}; B₂ = {2,6,7}; d₂ = (x,1,x₃,x₄,x₅,0,0)

 

 

6. А – не выполняется à $ `d₂

8. S₂ ¹ Æ

10. B выполняетсяà 0 + [a₉₅ = 1] > 0 à x₅ = 0

S₂ = {1,3,4}; B₂ = {2,5,6,7}; d₂ = (x,1,x₃,x₄,0,0,0)

 

 

 

6. А – не выполняется à $ `d₂

8. S₂ ¹ Æ

10. B выполняетсяà –3 + [a₈₄ = –3] = 0 >  –1 à x₄ = 1

S₂ = {1,3}; B₂ = {2,4,5,6,7}; d₂ = (x,1,x₃,1,0,0,0)

 

 

6. А – не выполняется à $ `d₂

8. S₂ ¹ Æ

10. B выполняетсяà –3 + [a₆₃ = –3] = 0 > –1 à x₃ = 1

S₂ = {1}; B₂ = {2,3,4,5,6,7}; d₂ = (x,1,1,1,0,0,0)

 

 

6. А – не выполняется à $ `d₂

8. S₂ ¹ Æ

10. B выполняетсяà 0 + [a₁₁ = 1] > 0 à x₁ = 1

S₂ = Æ; B₂ = {1,2,3,4,5,6,7}; d₂ = (0,1,1,1,0,0,0)

 

 

6. А – не выполняется à d₂ допусимо.

S₂ = Æ

b₀ = 9 + 0 = 9

R = d₂

I = {0,1,2,3,4,5,6,7,8,9}

7. N = 1

4. N>0

6. A – не выполняется à d₁ – допустимый

 

8. S₁ ¹ Æ

10. B выполняетсяà –1 + [a₄₅ = –1] = 0 > –1à x₅ = 1

11. S₁ = {1,3,4,6,7} B₁={2,5}

d₁ = (x₁,0,x₃,x₄,1,x₆,x₇)

 

 

 

6. А выполняется.

(i = 9; 0 = F₉(S₁) > F₉(B₁) = –1) à d₁ – недопустимо

7. N = 0

4. N > 0

min S = 9

R = d₂ = (0 1 1 1 0 0 0)

 

Контрольные вопросы для организации проверки усвоения изучаемого материала

Построить модель задачи о планировании производства.(Dantzig G.B. 1951г.)

 

Построить модель задачи о загрузке станков.( Dantzig G.B. 1951г.)

 

Построить модель задачи о транспортных перевозках.(Hitchcock F.L. 1941г. Koopmans T.G. 1947г.)

 

Построить модель задачи о максимальном потоке в сети с ограниченными пропускными способностями каналов. (Ford L.R., Fulkerson P.R. 1962 г.)

 

Построить модель задачи о ранце.

 

Построить модель задачи о назначениях. (Konig D. 1912 г.)

 

Построить модель задачи о кратчайшем маршруте в сети. (Floud R. 1962 г.)

 

Построить модель задачи о замене оборудования.

 

Построить модель задачи распределения дополнительных ресурсов. (Bellman R. 1960 г.)

 

Геометрическая интерпретация задачи линейного программирования.

 

Доказать справедливость табличного алгоритма замены базисных переменных при решении задач линейного программирования симплекс-методом.

 

Описать симплекс-метод решения задачи линейного программирования.

 

Описать алгоритм решения транспортной задачи методом потенциалов.

 

Обосновать алгоритм задачи распределения ресурсов методом динамического программирования.

 

Построить модель полного времени обработки информации для n независимых процессов. (Johnson S.M. 1954г.)

 

Обосновать алгоритм Джонсона (Johnson S.M.1954г.) и обобщить его на трехэтапные работы.

 

Обосновать алгоритм определения последовательности, при которой наибольшее число требований обслуживается в заданные директивные сроки.

 

Доказать необходимые условия оптимального размещения файлов при поиске их через начало носителя.

 

Доказать формулу математического ожидания холостого перемещения носителя при поиске файлов по кратчайшему маршруту.

 

Доказать необходимые условия оптимального размещения файлов при поиске их по кратчайшему маршруту.

 

Описать алгоритм оптимального размещения файлов на внешнем носителе.

 

Построить модель задачи выбора из базового набора состава пакета прикладных программ согласно заданному критерию.

 

Описать алгоритм решения задачи линейного программирования с булевыми переменными.

Контрольные вопросы для организации
проверки усвоения изучаемого материала.
РК1 (6 неделя), РК2 (12 неделя).

Согласовать дополнительные ресурсы между четырьмя функциональными подсистемами. Известна зависимость T(X,N) - эффективность N-oй функциональной подсистемы, если ей выделено
 X - ресурсов. Считать целевую функцию ceпapaбeльнoй.

 

Задана топология сети и длина маршрута из состояния i в состояние  j - T(i,j). (1 – источник, 8 – адресат). Найти кратчайший маршрут из каждого пункта сети до адресата и определить длину этого маршрута. а) сеть ациклическая, б) сеть общего вида Т(i,j)=T(j,i).

 

Заданы топология и пропускные способности каналов замкнутой информационной сети T(i,j). Найти максимальный поток и минимальное сечение для пары источник - адресат (1 – источник,
 8 – адресат).

 

Для сети ЭВМ перераспределить вычислительные ресурсы, если известны потери С(i,j), связанные с функционированием i-го ресурса в j-ом узле.

 

Разработано 5 вариантов изделия, которое будет функционировать в двух различных условиях. Известна эффективность функционирования каждого варианта в любом из этих условий c(i,j).

Какому варианту следует отдать предпочтение, если изделие уникальное?

Какие варианты следует тиражировать, если решено выпустить партию изделий?

Рекомендовать стратегию применения этих вариантов.

Указать ситуацию внешней среды для самого неблагоприятного случая.

 

Процесс обработки информации состоит из трех последовательных операций, которым последовательно подвергаются 8 различных массивов. Известно A_ij - время выполнения операции i над массивом j. Минимизировать время процесса обработки информации.

 

Задано 3 процедуры, с помощью которых можно полностью реализовать алгоритм, состоящий из 3 операций. Известны
T(i,j) - время реализации i-ой процедурой j-ой операции,
S(i) - объем занимаемой памяти i-oй процедурой, S - объем занимаемой памяти выбранным набором процедур. Bыбpaть такой набор процедур, который минимизирует время выполнения алгоритма при ограничениях на объем занимаемой памяти.

 

ЛИТЕРАТУРА

 

Вагнер Г. Основы исследования операций. М. «Мир» 1972 г.
(в трех томах).

Венцель Е.С. Исследование операций. М. «Советское радио»
1972 г.

Вильсон А.Дж. Энтропийные методы моделирования сложных систем. М. «Наука» 1978 г.

Ниесов В.А. Задача рационального расположения массивов информации на магнитной ленте. “Кибернетика” № 4 1968 г.

Саати Т.Л. Математические методы исследования операций. М. «Воениздат» 1963 г.

Танаев В.С., Шкуба В.В. Введение в историю расписаний. «Наука» 1971 г.

Balas E., An Additive Algorithm for Solving Linear Programs with Zero-One Variables. Operation Research 13. (1965) 517-546.

Bellman R. Combinatorial processes and dynamic programming.Proc. of Sympos. in Appl. Math vol X.1960 217-249.

Floyd R. Algorithm 97, Shortest Path. Communication of the ASM 5.345 (1962).

Ford L.R., Fulkerson D.R. Flows in Networks, Princezon Univ. Press, 1962.

Hoffman A.J. Markowitz H.M. A Note of Shortest Path Assignment and Transportation Problems. Naval Research Logistic Quarterly 10 375-379 (1963).

Hu T.C. Revised Matrix Algorithms for Shortest Parts SIAM J. on Appl. Math 15 207-218 (1967).

Johnson S.M. Optimal two and three stage production schedules with set-up times included. Nav. Res. Log. Quart. 1 №1 (1954) 61-68.

Raimond J.F. An Algorithm for the exact Solution of the Machine Scheduling Problem. JBM New York Scientific Center. Rep. 320-2925, Jan 1968.

Smith W.E., Various optimizers for single stage production. “Navel Research Logistics Quat. v3 № 1-2 1956, 59-66.