Временная диаграмма СМО
Входящие стрелки снизу указывают на поступление требования.
Стрелки выходящие вверх обозначают уход требования.


![]()


![]()
![]()
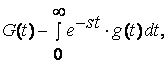
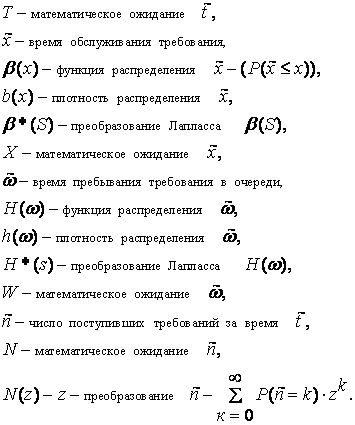
СМО типа M/G/1
Распределение числа требований N(z) в системе M/G/1
Предположим, что все требования обслуживаются в порядке поступления.
Установим связь между случайными величинами:
![]() –
число требований, остающихся в системе в момент ухода требования
–
число требований, остающихся в системе в момент ухода требования ![]() ;
;
![]() –
число требований, остающихся в системе в момент ухода требования
–
число требований, остающихся в системе в момент ухода требования ![]() ;
;
Рассмотрим два случая:
Первый имеет место, когда уходящее требование не оставляет
систему пустой, то есть ![]() .
.
![]() - время обслуживания
- время обслуживания ![]()
![]() .
.
![]() - число требований за
- число требований за ![]() .
.
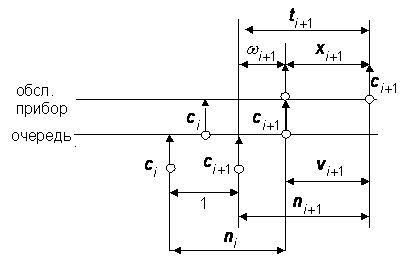
случай ![]()
Так как требования ![]() покидает
систему ,
покидает
систему ,
![]() .
.
Второй случай имеет место, требование ![]() оставляет систему пустой, то есть
оставляет систему пустой, то есть ![]() , тогда
, тогда
![]()
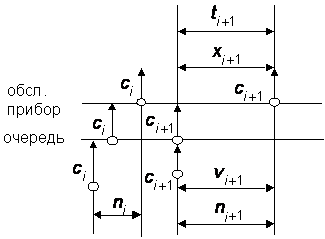
случай ![]()
Обобщая оба случая, приходим к выводу, что система M/G/1 характеризуется равенством:
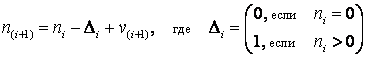 .
.
Определим производящую функцию случайной величины ![]() :
:
![]() .
.
и производящую функцию предельной
случайной величины ![]() :
:
![]() .
.
Образуем производящую функцию от полученного равенства
![]() ,
,
![]() .
.
Так как случайная величина ![]() -
число требований поступивших за
-
число требований поступивших за ![]() не зависит от
не зависит от ![]() – число требований в системе в момент ухода
требования
– число требований в системе в момент ухода
требования ![]() ,
тогда
,
тогда
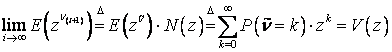 ,
,
где ![]() .
.
Так как входящий поток – пуассоновский, то имеем:
 .
.
Меняя порядок операций суммирования и интегрирования, получаем:

Так как 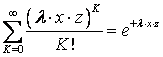 .
.
Определяем теперь преобразование Лапласа плотности времени
обслуживания:  .
.
Сравнивая ![]() , получим важный результат:
, получим важный результат:
![]() .
.
Преобразование Лапласа плотности вероятности времени
обслуживания в точке ![]() равно
производящей функции распределения вероятностей числа требований за время
одного обслуживания
равно
производящей функции распределения вероятностей числа требований за время
одного обслуживания ![]() .
.
Итак:
![]() ;
;
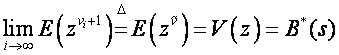 .
.
Теперь отдельно рассмотрим
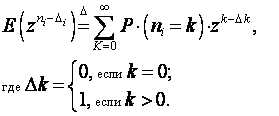

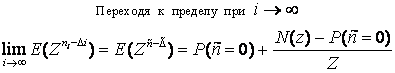
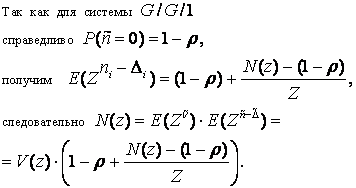
Решая относительно ![]() , получим первое уравнение Поллячика-Хинчина
для преобразований:
, получим первое уравнение Поллячика-Хинчина
для преобразований:
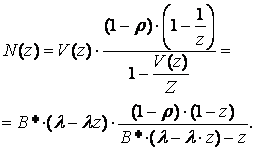
Рассмотрим ещё раз временную диаграмму СМО типа M/G/O, предполагая, что все требования обслуживаются в порядке поступления
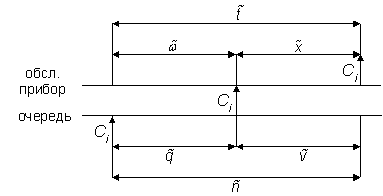
Дело в том, что соотношение
![]() .
.
справедливо между любыми случайными величинами, одну из которых можно отождествить с числом поступающих требований при пуассоновском потоке, а другую – с промежутком времени, в течение которого подсчитывается число поступающих требований, поэтому

что можно вывести и непосредственно.
Распределение времени пребывания в системе M/G/1
Учитывая ![]() , первое уравнение Поллячика-Хинчина можно
записать в виде:
, первое уравнение Поллячика-Хинчина можно
записать в виде:
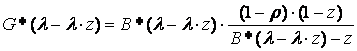 .
.
Введя замену переменной ![]() , имеем
, имеем

Это второе уравнение Поллячика-Хинчина для преобразований даёт выражение преобразования Лапласа распределения времени пребывания требования в системе.
Так как ![]() и учитывая, что
и учитывая, что ![]() – время обслуживания требования не зависит от
– время обслуживания требования не зависит от
![]() – времени
ожидания этого требования в очереди и, что при сложении двух независимых
случайных величин перемножаются преобразования Лапласа соответствующих функций
распределения, получаем третье уравнение Поллячика – Хинчина для
преобразования Лапласа распределения времени ожидания требования в очереди, то
есть
– времени
ожидания этого требования в очереди и, что при сложении двух независимых
случайных величин перемножаются преобразования Лапласа соответствующих функций
распределения, получаем третье уравнение Поллячика – Хинчина для
преобразования Лапласа распределения времени ожидания требования в очереди, то
есть

Различные производные производящей функции, вычисленные в точке z=1, дают возможность вычислить соответствующие моменты рассматриваемой случайной величины:

Точно также для непрерывных случайных величин можно найти
моменты, вычисляя в точке ![]() соответствующие производные преобразования
Лапласа рассматриваемой случайной величины:
соответствующие производные преобразования
Лапласа рассматриваемой случайной величины:
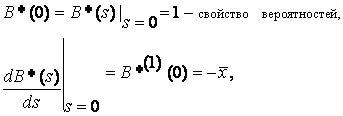
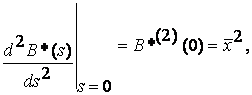
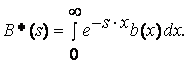
Используем теперь равенство для получения моментов случайной
величины ![]() :
:
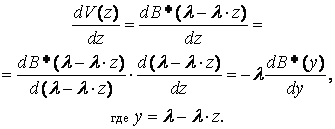
Полагая теперь ![]() , то есть
, то есть ![]() , имеем
, имеем
![]() .
.
Мы получили хорошо обоснованное заключение о том, что
ожидаемое число поступающих требований за время одного обслуживания равно ![]() , что согласуется с
полученными ранее результатом для G/G/1.
, что согласуется с
полученными ранее результатом для G/G/1.

Уравнение Поллячика-Хинчина для преобразований позволяет найти моменты распределения числа требований в системе:
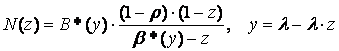 .
.



![]()


Дисперсия случайной величины x или второй центральный момент
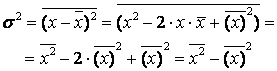
здесь:
![]() –
второй начальный момент;
–
второй начальный момент;
![]() –
квадрат первого начального момента;
–
квадрат первого начального момента;
Если обозначить:
 –
нормированная дисперсия;
–
нормированная дисперсия;
![]() –
стандарт;
–
стандарт;
 –
коэффициент вариации;
–
коэффициент вариации;
То учитывая:
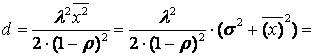

Это и есть результат, к которому мы стремились. Это выражение представляет собой среднее число преобразований в системе M/G/1, которое обычно называют формулой Поллячика - Хинчина для среднего значения.
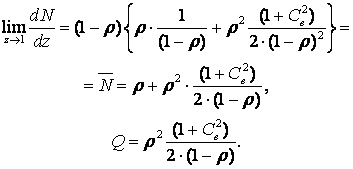
Среднее число преобразований в очереди![]()
 ,
,
так как из анализа системы G/G/1 следует, что
![]() .
.
В качестве примера применения формулы Поллячика–Хинчина рассмотрим систему M/M/1
 .
.
В качестве второго примера рассмотрим регулярное обслуживание, то есть систему M/D/1
 .
.
Таким образом, система типа М/D/1 содержит на 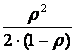 требований меньше, чем
система М/М/1.
требований меньше, чем
система М/М/1.
Для системы M/Er/1
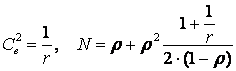 .
.
Это позволяет сделать вывод, что
![]() .
.
Задача 1:
Вычислительная сеть M/D/1 обслуживает поток задач, запросы на выполнение которых поступают в случайные моменты времени (в среднем 9 требований в час). На решение одной задачи необходимо 5 минут.
Определить математическое ожидание:
Времени реакции системы на запрос – ![]() .
.
Времени ожидания в очереди – ![]() .
.
Числа требований в системе – ![]() .
.
Числа требований в очереди – ![]() .
.
Числа требований в обслуживающем приборе – ![]() .
.
Если в качестве модели системы выбрать модель M/D/1.
![]()
![]()
![]()
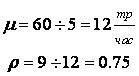

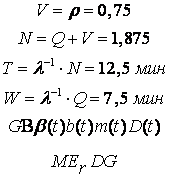
|
|
|
|
|
|
|
|
|
M/M/1 |
3 |
2,25 |
0,75 |
20 |
15 |
5 |
|
M/D/1 |
1,875 |
1,125 |
0,75 |
12,5 |
7,5 |
5 |
|
M/Er/1 |
2,438 |
1,688 |
0,75 |
16,25 |
11,25 |
5 |
Для системы G/G/m Кингман получил следующую оценку времени ожидания в очереди:
 ,
,
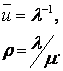
![]() –
дисперсия промежуточного интервала времени между прибытиями;
–
дисперсия промежуточного интервала времени между прибытиями;
![]() –
дисперсия времени обслуживания;
–
дисперсия времени обслуживания;
![]() –
математическое ожидание времени обслуживания;
–
математическое ожидание времени обслуживания;
![]() –
математическое ожидание интервала между прибытиями;
–
математическое ожидание интервала между прибытиями;
![]() –
коэффициент обслуживания.
–
коэффициент обслуживания.
Численные исследования показывают, что приближения
ухудшается с увеличением ![]() и
и
![]() , и улучшается с
увеличением
, и улучшается с
увеличением ![]() .
.