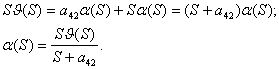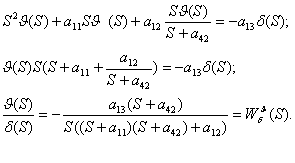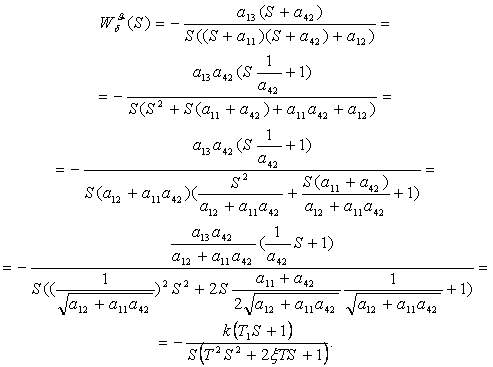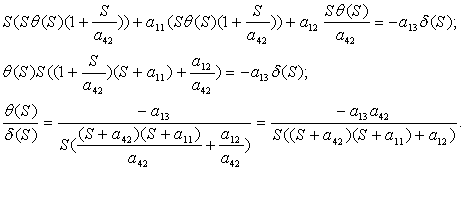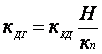Московский
Государственный Технический Университет имени Н.Э. Баумана
УТВЕРЖДАЮ
"___"__________2005 г.
____________________
Название документа
(тип документа)
(вид носителя)
_________19_________
(количество листов)
"
" ______ 2005 г.
___________________
Москва – 2005
Содержание
Введение. Ошибка! Закладка не определена.
1. Функции и
структура АСУТП комбинированного типа. 4
1.1. Функциональная
схема системы.. 5
1.2. АСУТП с
информационным типом функционирования. 6
1.3. АСУТП с
функционированием в режиме советчика. 7
1.4. АСУТП в
режиме непосредственного цифрового управления. 7
2. Математическая
модель системы.. 8
2.1. Объект
управления. 8
2.2. Измерительные
устройства системы.. 14
2.2.1. Авиагоризонт. Ошибка! Закладка не определена.
2.2.2. Датчик
угловой скорости.. Ошибка! Закладка не определена.
2.2.2.1
Функциональная схема…………...………………………………………....................14
2.2.2.2
Математическая модель………………………………………………………….……15
2.3. Исполнительное
устройство. Ошибка! Закладка не определена.
2.3.2.1
Функциональная схема…………...………………………………………....................16
2.3.2.2
Математическая модель……………………………………………………………..…16
2.4. Человек-оператор. 16
2.5. Бортовой
вычислительный комплекс. 18
2.6. Математическая
модель АСУТП в комплексной области. 20
Список литературы.. 21
Введение.
Для выполнения домашнего задания
по курсу « Управление сложными системами» рассмотрим понятие –
Автоматизированная Система Управления
Техническим Процессом (АСУ ТП). АСУ ТП – характерный представитель сложных
систем и занимает особое место из множества автоматизированных систем, так как
АСУ ТП непосредственно управляет процессом. АСУ ТП – это человеко-машинная
система, обеспечивающая сбор и обработку информации для оптимизации управления
техническим (технологическим) процессом или объектом в соответствии с выбранным
критерием.
Перейдем к понятию –
Математическая Модель (ММ). Любую задачу управления необходимо сформулировать
математически (особенно на этапе принятия решений), что содержит три элемента:
ММ, критерий управления и учет ограничений.
Математическая модель – это
совокупность математических соотношений, описывающих поведение объекта и те
условия, в которых он работает. То есть любая математическая модель
представляет собой приближенное описание какого-либо класса явлений реального
мира, выраженное с помощью математических символов. Особенностями ММ являются
неадекватность и трудоемкость. Неадекватность обусловлена неточностью описания
реальных процессов и неточностью реализации ММ при закладке ее в вычислительную
машину. Время на разработку ММ составляет до 80% от всего времени решения
задачи, кроме того ММ уточняется в процессе работы системы, поэтому составление
ММ – достаточно трудоемкий процесс. Наиболее удобной формой ММ системы для
расчета частотным методом является структурная схема, которая может быть
получена на основе передаточных функций отдельных звеньев, образующих систему.
Задачи управления самолетом
включают стабилизацию центра масс на заданной траектории и стабилизацию
углового положения самолета относительно центра масс. Наиболее жесткие
требования к точности управления предъявляются на этапах взлета и посадки.
Ограничения на траектории движения при этом обусловлена наличием препятствий в
секторах взлета и посадки. Препятствия находятся на земле, поэтому результатом
исследования процессов взлета и посадки должна быть траектория движения
относительно земли. То есть в число входных переменных обязательно должны быть
включены координаты центра масс самолета в земной системе координат.
В то же время выбор
переменных состояния объекта в значительной степени произволен, и выходные
величины не обязательно должны совпадать с переменными состояния. Этим
обусловлено большое число вариантов математических моделей, описывающих
движение самолета.
Методы построения ММ весьма
разнообразны: от использования физических закономерностей протекания
технологических процессов, экспертно модифицированных с помощью эмпирических
оценок, до универсальных методов группового учета аргументов, полностью ориентированных
на использование опытных данных по технологическому процессу и применения ЭВМ
как интеллектуального инструмента.
В настоящее время
большинство ММ действующих АСУТП построено с помощью методов, лежащих между
этими двумя границами. Они характеризуются тем, что структуру ММ определяет
исследователь, а коэффициенты модели находят методами корреляционного и регрессивного
анализа, математического эксперимента, теории чувствительности.
1. Функции и структура АСУТП комбинированного типа
АСУ ТП – это человеко-машинная
система, обеспечивающая сбор и обработку информации для оптимизации управления
техническим (технологическим) процессом или объектом в соответствии с выбранным
критерием.
Для АСУ ТП различают три основные
функции:
1)
Информационная
– сбор, обработка, передача и предоставление информации в управляемом процессе
персоналу.
2)
Управляющая
– выработка управления в соответствии с определённым критерием и его
реализация.
3)
Вспомогательная
– обеспечивает работу технических и программных средств.
Для лучшего понимания
представленных в дальнейшем функциональных схем сначала покажем обобщенную
функциональную схему АСУ ТП:
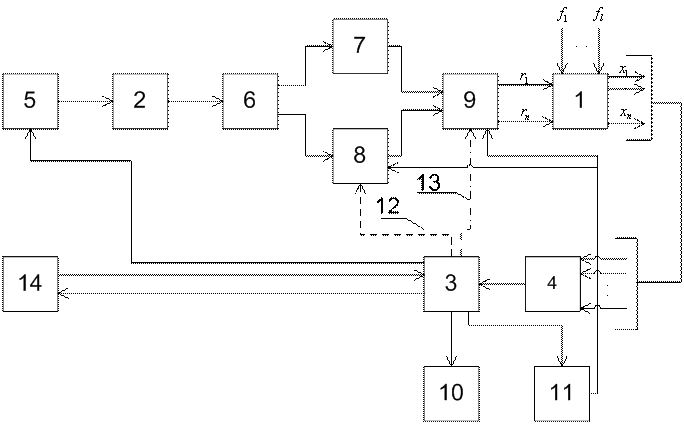
Рис1. Типовая структура
На этом рисунке:
r1,
… rm – регулирующее (управляющее)
воздействие;
x1,
x2,
… xn – регулируемые переменные;
f1, … fl
– возмущающее воздействие;
1 – объект управления;
2
–
человек-опереатор;
3 – вычислительный комплекс;
4 – датчики информации;
5 – система отображения
информации;
6 – пульт управления;
7 – устройство логического
управления;
8 – локальные регуляторы;
9 – исполнительные устройства и
органы управления;
10
– система
сигнализации;
11 – система аварийной защиты;
12,
13 –
функциональные связи;
14 – АСУ более высокого уровня.
1. 1. Функциональная схема системы
Функциональная схема системы управления
продольным движением самолёта относится к классу АСУ ТП комбинированного типа.
Система управления продольным движением самолета
является подсистемой сложной структуры пилотажного комплекса самолета. Этот
комплекс управляет угловым движением самолета относительно трех взаимно
перпендикулярных осей, а также удержанием его центра масс на заданной опорной
траектории (за определение опорной траектории отвечает навигационный комплекс).
Функциональная схема представлена
на рисунке 2:
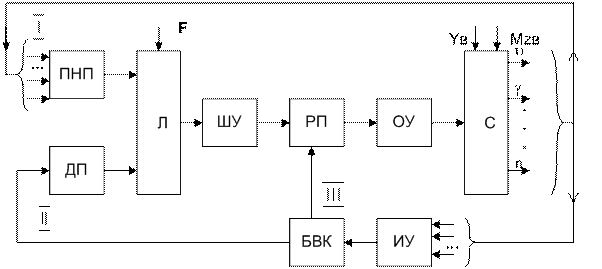
Рис. 2. Функциональная схема АСУ ТП комбинированного типа.
J -
действующее значение угла тангажа;
MZB – возмущающий момент;
ПНП – пилотажные навигационные
приборы;
ДП – директорный прибор;
Л – лётчик;
ШУ – штурвал управления;
РП – рулевой привод;
ОУ – органы управления;
БВК – бортовой вычислительный
комплекс;
ИУ – измерительные устройства;
С – самолёт.
Система может функционировать в
трёх режимах: информационном (ручном) – контур I, в режиме «советчика»
(полуавтоматическом) – контур II
и автоматическом режиме – контур III.
1. 2. АСУТП с информационным типом
функционирования
При функционировании АСУТП в
информационном (ручном) режиме (контур I) (рис.2) летчик, анализируя показания
пилотажных навигационных приборов (ПНП), принимает решение, вырабатывает
команду и с помощью штурвала управления (ШУ), рулевого привода (РП) и органов
управления (ОУ) воздействует на движение самолета.
Предположим, что при ручном пилотировании (контур I) в
режиме стабилизации лётчик (Л) обязан поддерживать заданный наклон продольной
оси самолёта к горизонту, т.е. значение требуемого угла тангажа Jз ему известно. Тогда, если под действием возмущающего
момента MZв самолет
поворачивается относительно оси OZ, то пилот на основе показаний авиагоризонта
определяет действительное значение угла J и отклонение DJ=(J–Jз). В результате лётчик вырабатывает команду Kc=k×(J – Jз), отрабатывает её, перемещая штурвал управления (ШУ).
Рулевой привод (РП) отклоняет органы управления (ОУ) – рули высоты (РВ) и под
действием управляющего момента восстанавливает требуемое значение угла тангажа JЗ.
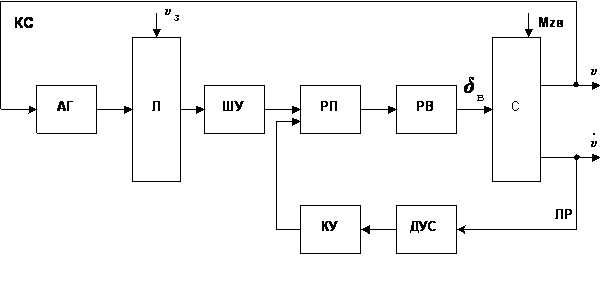

Рис. 3. Схема ручного управления системой.
В режиме управления задача лётчика усложняется.
Например, при обеспечении заданной высоты полёта лётчик так же в результате
сравнения J и Jз должен
выработать команду управления , компенсирующую отклонение центра масс С. Однако
значение угла Jз лётчик должен
рассчитать на основе показаний ПНП, таких как высотомер, вариометр и
авиагоризонт. При этом команда и свойства системы зависят от опыта лётчика, его
индивидуальных особенностей и состояния.
Внутренний
контур – ЛР –предназначен для улучшения динамических свойств самолёта. Он
содержит ДУС, который измеряет изменения угловой скорости 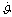 , и КУ, которое воздействует на РП. В результате пилот
достигает нужного значения угла тангажа с меньшими колебаниями самолёта, при
достижении этого значения. ЛР помогает лётчику вести самолёт более плавно
, и КУ, которое воздействует на РП. В результате пилот
достигает нужного значения угла тангажа с меньшими колебаниями самолёта, при
достижении этого значения. ЛР помогает лётчику вести самолёт более плавно
В общем случае можно сказать, что основные
характеристики системы определяются возможностями человека-оператора (летчика) в получении, переработке и использовании
информации.
1. 3. АСУТП с функционированием в режиме
советчика.
На рисунке 1 вычислительный
комплекс 3 на основе математической модели и критерия управления рассчитывает
возможные варианты решений (управляющих действий) человека-оператора (даёт
советы) через систему отображения информации 5. Человек-оператор выбирает одно
из них и воздействует на процесс и объект управления 1 через технические
средства 7-9.
На рисунке 2 это контур II. АСУ ТП функционирует при этом в
режиме «советчика». АСУ ТП содержит БВК и ДП или систему отображения
информации. Параметры самолёта через ИУ поступают на БВК, который анализирует
эту информацию, определяет оптимальные решения и выдаёт рекомендации (советы)
по управления самолётом на ДП. При этом наиболее простым является режим
слежения с компенсацией. Так для рассмотренного выше режима управления
самолётом лётчик, наблюдая по командному (директорному) прибору сигнал
рассогласования DJ,
сводит его к нулю, отклоняя в нужном направлении ШУ. Так как пилот выполняет
команды от БВК, то его задача в управлении самолётом заметно упрощается.
1. 4. АСУТП в режиме непосредственного цифрового
управления.
В данном режиме ВК рассчитывает
не варианты оптимальных решений, как в предыдущем случае, а вырабатывает
непосредственные управляющие воздействия. Такой режим также возможно
реализовать на ЛА. В этом случае (контур III) БВК будет выполнять функции
непосредственного (прямого) цифрового управления. В соответствии с целью
управления и действительными значениями переменных, характеризующих угловое
положение корпуса и движение центра масс С, БВК рассчитывает требуемые значения
управляющих воздействий и подает соответствующие сигналы непосредственно в
рулевой привод.
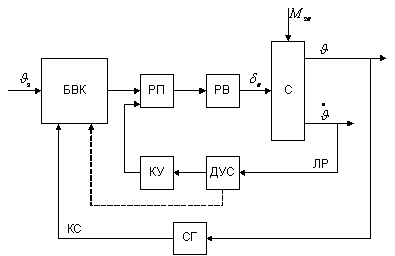
Рис. 4. Система стабилизации для автоматического
управления.
Летчик в этом режиме осуществляет
контроль за работой системы, и при неудовлетворительном функционировании
цифровой автоматической системы (ЦАС) – коррекцию управляющей программы или
перевод АСУТП в один из рассмотренных выше режимов.
В ЦАС стабилизации также входит
ЛР (Рис.4). Если ДУС имеет цифровой выход, то сигнал (штриховая линия на рис. 4),
пропорциональный угловой скорости тангажа 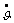 , подается на БВК. БВК при этом выполняет функцию дискретного
корректирующего устройства системы.
, подается на БВК. БВК при этом выполняет функцию дискретного
корректирующего устройства системы.
2. Математическая модель системы.
2. 1. Объект управления.
Объектом управления в рассматриваемой
системе является самолет. Получим упрощенные уравнения динамики самолета при
следующих допущениях:
а) пренебрегаем вариациями
скорости 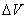 и влиянием силы
тяжести;
и влиянием силы
тяжести;
б) будем рассматривать самолет
статически устойчивым; как твердое тело постоянной массы m.
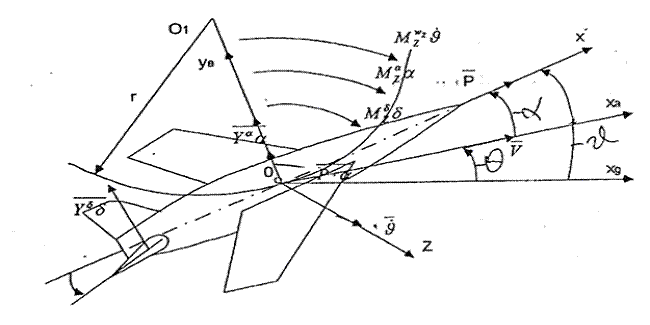
Рис.
5. Силы и моменты, действующие на самолет
На рис. 5 показаны основные силы
и моменты, действующие на самолет в продольной плоскости. Положительные
направления отсчета углов атаки 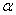 , тангажа
, тангажа 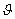 , угла наклона касательной к траектории
, угла наклона касательной к траектории 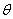 , отклонения руля
высоты
, отклонения руля
высоты 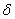 приняты против часовой
стрелки, если смотреть с оси OZ.
приняты против часовой
стрелки, если смотреть с оси OZ.
Тогда уравнение моментов в
продольной плоскости ЛА (относительно оси OZ связанной системы координат) будет
иметь следующий вид:
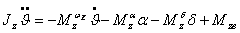 , (1.1)
, (1.1)
где 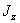 - момент инерции ЛА
вокруг оси OZ,
- момент инерции ЛА
вокруг оси OZ,
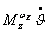 - момент демпфирования;
- момент демпфирования;
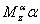 - флюгерный момент;
- флюгерный момент;
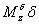 - управляющий момент;
- управляющий момент;
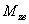 - возмущающий момент;
- возмущающий момент;
 ,
, 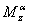 ,
, 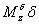 - частные производные момента тангажа
- частные производные момента тангажа 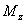 , соответственно по
параметрам
, соответственно по
параметрам 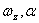 и
и 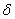 .
.
С учетом рис. 5, на основании
2-го закона Ньютона получим уравнение сил:
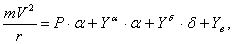 (1.2)
(1.2)
где r - радиус кривизны траектории
движения центра масс ЛА.
В правой части уравнения (1.2)
записаны составляющие на ось 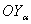 , создаваемые соответственно силой тяги двигателя P,
подъемной силой крыльев
, создаваемые соответственно силой тяги двигателя P,
подъемной силой крыльев 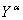 и органами управления
и органами управления 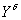 , а также возмущающая сила
, а также возмущающая сила 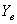 . При этом учтено, что угол атаки для самолетов обычно не
превышает 20°.
. При этом учтено, что угол атаки для самолетов обычно не
превышает 20°.
К уравнениям (1.1) и (1.2)
следует добавить еще уравнение
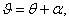 (1.3)
(1.3)
определяющее связь в продольной
плоскости между скоростной 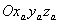 и связанной
и связанной 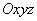 системами координат.
системами координат.
Уравнения (1.1)-(1.3), в общем
случае являются нелинейными и нестационарными. Однако их можно считать
линейными с учетом гипотезы малости отклонений параметров от их значений для
некоторого теоретического не возмущенного движения (эти значения могут быть
найдены путем численного интегрирования уравнений движения самолета).
Тогда, разделив уравнение (1.1)
на 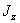 , а уравнение (1.2) на
, а уравнение (1.2) на 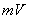 и учитывая, что
и учитывая, что 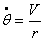 , получим:
, получим:
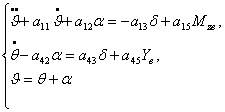 (1.4)
(1.4)
В системе уравнений (1.4).индекс
приращения  перед переменными
перед переменными 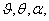 ... опущен.
... опущен.
Здесь 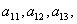 ...- динамические коэффициенты, характеризующие основные
динамические свойства ЛА, соответственно демпфирование (регулирование),
статическую устойчивость, эффективность органов управления и т.д.
...- динамические коэффициенты, характеризующие основные
динамические свойства ЛА, соответственно демпфирование (регулирование),
статическую устойчивость, эффективность органов управления и т.д.

Динамические коэффициенты
являются известными функциями времени, так как они зависят от параметров,
соответствующих некоторой невозмущенной траектории.
Анализ продольного углового
возмущенного движения ЛА показывает, что оно является короткопериодическим. При
этом за время переходного процесса, длящегося обычно доли секунды или несколько
секунд, переменные коэффициенты уравнений (1.1) и (1.2) не успевают заметно
измениться. Поэтому возможно применение метода "замораживания"
коэффициентов.
Применим к системе (1.4)
преобразование Лапласа при нулевых начальных условиях:
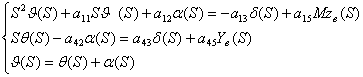 (1.4`)
(1.4`)
Таким образом, уравнения (1.4`)
позволяют найти передаточные функции 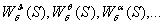 , определяющие основные динамические и статические свойства
ЛА по управляющему (управляемость) и возмущающему (устойчивость) воздействиям.
, определяющие основные динамические и статические свойства
ЛА по управляющему (управляемость) и возмущающему (устойчивость) воздействиям.
Мы будем искать
передаточные функции 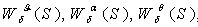 которые определяются
через входное воздействие на систему d, поэтому остальные воздействия МZB и YB надо приравнять к 0.
Так как Yd<<Ya (площадь рулей высоты во много меньше, чем площадь крыльев и
значит подъёмная сила крыльев во много раз больше, чем у рулей высоты), то
коэффициентом а43 можно пренебречь, то есть а43=0. В
результате получим следующую систему уравнений:
которые определяются
через входное воздействие на систему d, поэтому остальные воздействия МZB и YB надо приравнять к 0.
Так как Yd<<Ya (площадь рулей высоты во много меньше, чем площадь крыльев и
значит подъёмная сила крыльев во много раз больше, чем у рулей высоты), то
коэффициентом а43 можно пренебречь, то есть а43=0. В
результате получим следующую систему уравнений:
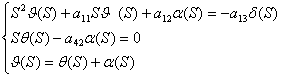
Умножим третье уравнение системы
на S:
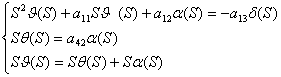 (1.4``)
(1.4``)
Объединяя второе и третье
уравнения, получим:
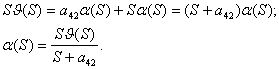
Подставим последнее выражение в
первое уравнение системы (1.4`):

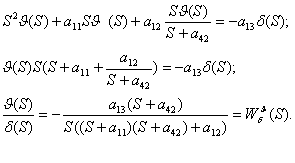
Таким образом найдена
передаточная функция, отражающая влияние управляющего воздействия на угол
тангажа 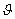 .
.
Преобразуем полученное выражение:
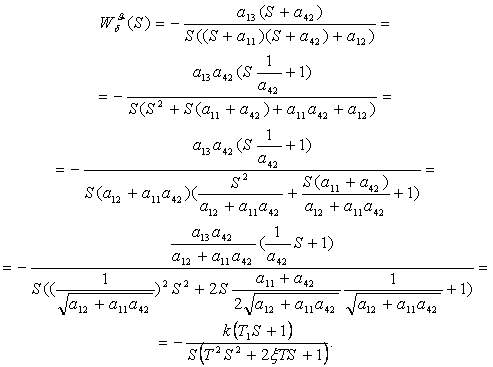
Поясним введенные обозначения
коэффициентов.
k - коэффициент передачи С,
характеризующий его маневренность,
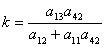 , 1/с.
, 1/с.
С увеличением высоты полета
коэффициент k уменьшается. Маневренность ЛА ухудшается также с увеличением
степени статической устойчивости.
Т1, Т - постоянные времени,
определяющие соответственно инерционные свойства ЛА при создании нормальной
перегрузки и собственную частоту колебаний самолета,
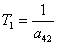 , с;
, с;
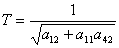 ,с.
,с.
Постоянная времени Т определяется
главным образом конструктивными размерами ЛА, а также степенью статической
устойчивости, скорости и высотой полета.
x -
коэффициент относительного демпфирования короткопериодической составляющей
возмущенного движения самолета,
 .
.
Известно, что оптимальным
значением коэффициента x для колебательного процесса
является x=0,7. Однако, конструктивные возможности увеличения
градиента 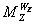 ограничены. Кроме того,
коэффициент x уменьшается с увеличением высоты
и числа M=V/a, где a - скорость звука. Это привело бы к резкому увеличению
колебательности переходных процессов.
ограничены. Кроме того,
коэффициент x уменьшается с увеличением высоты
и числа M=V/a, где a - скорость звука. Это привело бы к резкому увеличению
колебательности переходных процессов.
Локальный регулятор ЛР (см. рис. 3,
4) предназначен для улучшения пилотажных характеристик самолета. Требуемое
значение коэффициента затухания xд системы самолет-демпфер
обеспечивается соответствующим выбором параметра настройки системы -
коэффициента передачи ДУСа.
Проведем аналогичные выводы для
получения передаточных функций 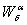 и
и 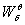 .
.
Для получения 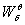 из второго и третьего
уравнений системы (1.4``):
из второго и третьего
уравнений системы (1.4``):

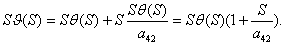
Воспользуемся этим уравнением для
преобразования первого уравнения системы (1.4``):
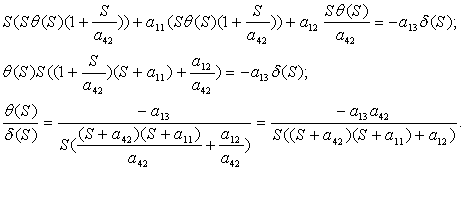
Таким образом:
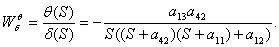
Приведем это выражение к
описанным выше коэффициентам.


Для вывода 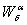 воспользуемся
полученным ранее уравнением
воспользуемся
полученным ранее уравнением
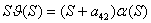
и подставим его в первое
уравнение системы:

Преобразуем выражение:

2.2. Измерительные
устройства системы.
Измерительные
устройства системы (датчики) поставляют информацию о движении самолёта лётчику
или БВК (рис. 2). На основании предоставленной информации принимается решение.
К измерительным устройствам относятся: авиагоризонт, датчик угловой скорости и
другие.
2.2.1. Авиагоризонт.
Авиагоризонт
входит в состав пилотажных навигационных приборов (ПНП) (рис.2) в контур I. Также авиагоризонт входит в
схему ручного пилотирования самолётом (рис.3). На основании показаний этого
прибора лётчик может определить, например, действительное значение угла тангажа
J и сравнить его с заданным.
Авиагоризонт
предназначен для определения пространственного положения летательного аппарата
по крену и тангажу, бокового скольжения и индикации команд управления по крену
и тангажу.
АГ построен на базе трехстепенного или свободного
гироскопа и является практически безинерционным устройством. Следовательно, его
математическую модель можно принять в виде
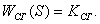
В дальнейшем примем Ксг = 1 и не будем
явно обозначать его в математической модели системы.
2.2.2.
Датчик угловой скорости.
2.2.2.1. Функциональная
схема.
Датчик угловой
скорости (ДУС) предназначен для измерения угловой скорости вращения самолёта.
ДУС сконструирован на основе двухстепенного гироскопа (рис. 6).
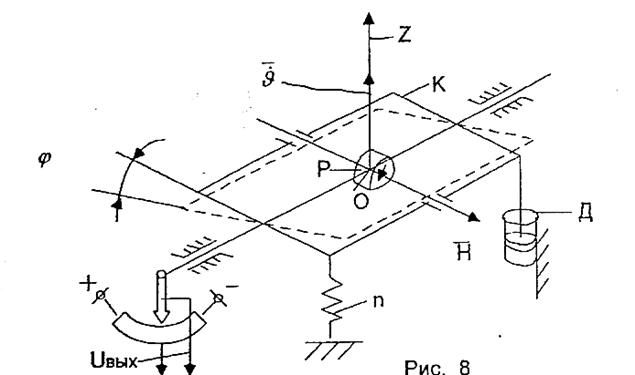
Рис. 6 Функциональная схема ДУС
Если корпус самолёта поворачивается,
например, вокруг оси OZ
с некоторой угловой скоростью 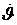 , то эту скорость можно рассматривать как угловую скорость
вынужденной прецессии ротора Р гироскопа. В результате появится гироскопический
момент Мг=Н
, то эту скорость можно рассматривать как угловую скорость
вынужденной прецессии ротора Р гироскопа. В результате появится гироскопический
момент Мг=Н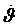 , где Н – кинетический момент ротора. Под действием этого
момента кожух гироскопа К будет поворачиваться до тех пор, пока Мг
не будет уравновешен моментом пружины П и моментом локального регулятора Д.
, где Н – кинетический момент ротора. Под действием этого
момента кожух гироскопа К будет поворачиваться до тех пор, пока Мг
не будет уравновешен моментом пружины П и моментом локального регулятора Д.
2.2.2.2. Математическая
модель.
Упрощённое
уравнение движения ДУСа можно записать в следующем упрощённом виде:
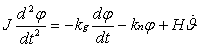 (2.1)
(2.1)
где J – момент инерции ДУСа
относительно оси кожуха;
j - угол поворота кожуха;
кg, кп – передаточные
коэффициенты, соответственно локального регулятора Д и пружины.
Математическая модель измерителя, согласно
[1], может быть принята в следующем
виде:
Wдг(S)=kдг.
Здесь 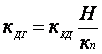 - коэффициент передачи
ДУСа;
- коэффициент передачи
ДУСа;
кпд -
передаточный коэффициент из уравнения потенциометрического датчика ПД: Uвых= кпд*j.
2.3. Исполнительное устройство.
Исполнительным устройством является
рулевой привод. Рулевой привод служит для перемещения органов управления (рулей
высоты и т.д.) самолетом. Одним из основных устройств РП является рулевая
машинка РМ. Предварительный усилитель, РМ и
элементы обратной связи образуют РП. В зависимости от вида используемой
энергии РМ и соответственно РП делят на электрические, гидравлические,
пневматические и на горячем газе. На самолетах чаще всего используются
гидравлические РП.
2.3.1.
Функциональная
схема.
На Рис.6 приведена функциональная схема
гидравлического РП.
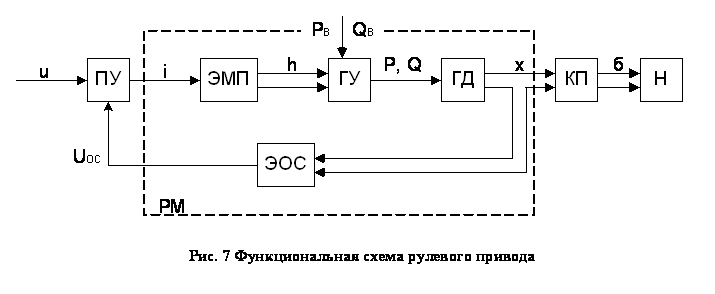
Управляющий сигнал U поступает на вход
предварительного усилителя (ПУ) (полупроводникового, магнитного или др.), в
котором суммируется с сигналом обратной связи Uос и усиливается.
Электромеханический преобразователь (ЭМП) (обычно это электромеханическое реле
с пропорциональным управлением) преобразует электрический сигнал i в механическое перемещение h (или поворот a) управляющего устройства ( золотника, заслонки,
струйной трубки) гидроусилителя (ГУ). Гидроусилитель управляет расходом Q и давлением Р масла на входе в гидродвигатель
(ГД). Гидродвигатель (поступательного или поворотного действия) перемещает
нагрузку Н - рули высоты, руль направления или элероны через кинематическую
передачу (КП) - проводку.
Для придания РП определенных
динамических свойств применяются различные обратные связи ОС: жесткая,
скоростная или изодромная. Элементом главной жесткой обратной связи ЭОС
является потенциометрический датчик. В ПУ, ГУ, ГД могут применяться местные ОС.
2.3.2.
Математическая модель
Можно считать,
что гидравлический РП с жесткой ОС не вносит существенных динамических
искажений в районе частоты среза системы стабилизации. Это позволяет иногда при
расчете контура стабилизации не учитывать динамику гидравлического РП и
принимать передаточную функцию привода в замкнутом состоянии, согласно [1], в виде
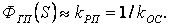 , где
, где 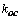 - коэффициент
передачи обратной связи.
- коэффициент
передачи обратной связи.
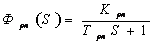 Более сложной математической моделью, согласно [1],
учитывающей полосу пропускания РП, является,
Более сложной математической моделью, согласно [1],
учитывающей полосу пропускания РП, является,
где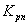 - коэффициент передачи рулевого привода;
- коэффициент передачи рулевого привода; 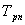 – период собственных колебаний РП.
– период собственных колебаний РП.
2.4.
Человек-оператор.
При ручном пилотировании самолета
летчик находится в прямой цепи АСУТП (см. рис.2) и является одним из ее
звеньев. Следовательно, динамические характеристики системы будут зависеть от
возможностей пилота с точки зрения получения, переработки и использования
информации.
Рис.8 Модель человека-оператора
Применение информационного
подхода позволяет получить линейную "модель" человека-оператора (см.
рис. 8) для режима слежения с компенсацией.
Летчик получает информацию с
помощью сенсорного "входа", представляющего собой совокупность
анализаторов (зрительного, слухового, вестибулярного аппарата и др.). Этот этап
может быть описан запаздывающим звеном 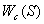 . Значение
. Значение 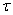 лежит в пределах
0,2…0,5 с.
лежит в пределах
0,2…0,5 с.
Этап анализа полученной
информации и принятия решения характеризуется передаточной функцией 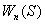 . При этом инерционность летчика определяется постоянной
времени апериодического звена
. При этом инерционность летчика определяется постоянной
времени апериодического звена 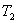 , которая обычно не превышает 10 секунд. Человек-оператор
стремится компенсировать эту инерционность, что отражается в передаточной
функции
, которая обычно не превышает 10 секунд. Человек-оператор
стремится компенсировать эту инерционность, что отражается в передаточной
функции 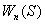 дифференцирующим
звеном первого порядка с постоянной времени
дифференцирующим
звеном первого порядка с постоянной времени 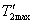 =1с. Для опытного пилота можно принять
=1с. Для опытного пилота можно принять 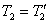 , поэтому
, поэтому 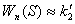 .
.
В результате латентный, или
скрытый, период реакции летчика представляется произведением:
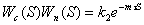 ,
,
где 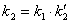 .
.
Передаточная функция 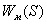 соответствует
моторному "выходу" пилота или этапу отработки определенной команды с
помощью штурвала управления. Этот процесс является инерционным с постоянной
времени
соответствует
моторному "выходу" пилота или этапу отработки определенной команды с
помощью штурвала управления. Этот процесс является инерционным с постоянной
времени 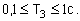
Летчик отрабатывает
последовательно все 3 этапа, поэтому 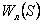 =
= 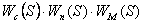 .
.
Следовательно, передаточная
функция летчика может быть записана следующим образом:
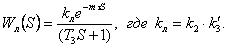 (2.2)
(2.2)
Следует отметить, что такое
представление является приближенным. Структура и параметры передаточной функции
человека-оператора зависят от характера выполняемой задачи, особенностей
объекта управления, состояния пилота и внешних воздействий.
Однако выражение (2.2) позволяет
оценить в линейной постановке влияние летчика на динамику исследуемой системы.
2.5. Бортовой вычислительный комплекс
Положение БВК в рассматриваемой
системе обозначалось ранее(Рис. 1).
Непрерывные сигналы с выхода
измерительных устройств через многоканальный коммутатор устройства ввода-вывода
БВК поступает на вход аналогово-цифрового преобразователя АЦП, где
преобразуются в цифровой код. Цифровое вычислительное устройство в соответствии
с программой (алгоритмом управления) производит над кодами чисел определенные
арифметические и логические операции. Результаты вычислений передаются в
цифроаналоговый преобразователь ЦАП, который преобразует цифровой сигнал в
аналоговый. Форма сигнала на выходе БВК определяется типом экстраполятора,
применяемого в ЦАП.
Процесс
преобразования сигналов в БВК связан с их квантованием по времени и уровню.
Величина интервала квантования по времени 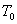 , в соответствии с теоремой Котельникова, должна быть меньше
или равна половине периода гармоники наивысшей частоты
, в соответствии с теоремой Котельникова, должна быть меньше
или равна половине периода гармоники наивысшей частоты 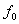 , содержащейся в непрерывном сигнале, т.е.
, содержащейся в непрерывном сигнале, т.е. 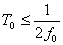 .
.
Интервал
квантования по уровню определяется количеством разрядов АЦП, ЦВУ и ЦАП. При
большом числе разрядов в линейном приближении математической модели БВК
квантованием по уровню можно пренебречь. Тогда БВК может быть охарактеризована
дискретной передаточной функцией D(Z).
Передаточная функция БВК отражает
программу переработки входной последовательности чисел у* в выходную х* и может
быть представлена, с учетом физической реализуемости, в виде
дробно-рационального выражения
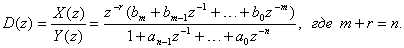
(2.7)
Отсюда на основании теоремы о
смещении аргумента получим разностное уравнение, определяющее алгоритм
управления, реализуемый БВК,
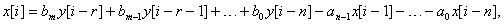 (2.8)
(2.8)
Структура и параметры передаточной
функции (2.7) или алгоритма управления (2.8) БВК определяются на этапе синтеза
системы.
Следует отметить, что реализацию
всех известных законов регулирования с помощью БВК в автоматической системе
угловой стабилизации самолета (Рис. 3) осуществить значительно проще, чем на
аналоговых корректирующих устройствах.
2.6.
Математическая модель АСУТП в комплексной области
Локальный регулятор ЛР в
структуре АСУТП является регулятором угловой скорости вращения самолета относительно поперечной оси OZ. При этом
динамические свойства самолета зависят от значения коэффициента передачи ДУСа
Кдг.
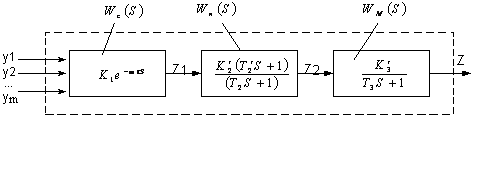
На Рис.9 представлена структурная
схема АСУТП, представляющая общую математическую модель системы в комплексной
области. Модель построена на основе передаточных функций описанных выше
элементов системы.
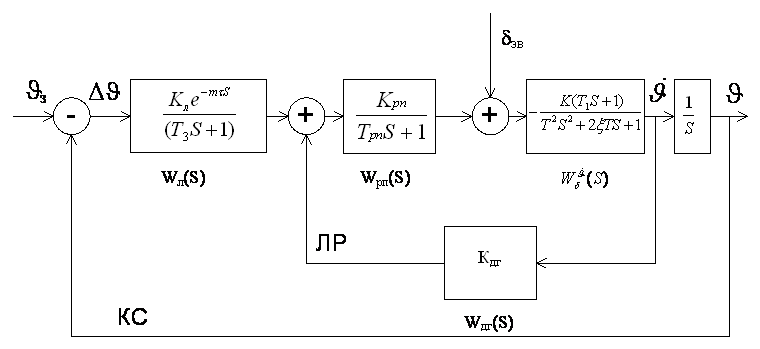
Рис. 9. Расчётная структурная схема системы.
Локальный регулятор предназначен
для гашения короткопериодических движений самолёта путём реализации обратных
связей по угловой скорости. Поэтому локальный регулятор должен включать
чувствительный элемент, реагирующий на угловую скорость (ДУС).
Локальный регулятор является неотъемлемой частью
системы управления самолётом, так как с его помощью улучшаются пилотажные
характеристики летательного аппарата.
Т.о. мы создали математическую модель
автоматизированной системы управления самолётом в комплексной области, которая
содержит математические модели человека-оператора, рулевого привода, локального
регулятора. Получая на вход системы Jз, на
выходе система имеет действительное значение угла тангжа.
Примечание: На Рис.9 не изображена передаточная функция АГ, занимающая
положение на главной обратной связи (см. 2.2.1, где мы обусловились не
обозначать явно её в математической модели системы).
1. Веселов А.П. Лекции по курсу "Управление
сложными системами".
2. Веселов А.П. А. Л. Волков, Е.Г. Ревункова. Расчет
автоматизированной системы управления техническим процессом (методические
указания). – М.: Эликс+, 2000.






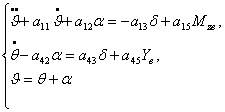

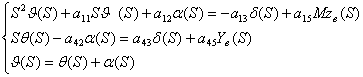
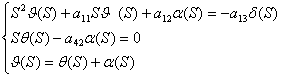
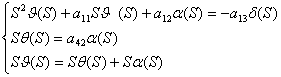 (1.4``)
(1.4``)