CD®B	- в аудитории одновременно может быть только один преподаватель;
AC®D	- каждый курс одновременно может читаться только в одной аудитории;
CE®A	- каждый студент одновременно может слушать только один курс;
A®B	- каждый курс ведет только один преподаватель;
CD®A	- в аудитории в один и тот же момент времени может читаться только один курс;
CB®D	- преподаватель в один и тот же момент времени может находиться только в одной аудитории;
AE®T	- по каждому курсу каждый студент имеет только одну оценку;
CE®D	- студент в один и тот же момент времени может находиться только в одной аудитории

)

Задача:

Построить ρ - хорошую схему БД.

1.2. Решение задачи.

1. Положим r=0, где r - множество схем отношений, которые образуют схему БД.

2. Определим минимальное покрытие G для F:

1) G = (CD®B, AC®D, CE®A, A®B, CD®A, CB®D, AE®T, CE®D)

2) A. Проверяем принадлежность X®A замыканию (G - X®A)⁺, где X®A G:

a) CD®B:

G - CD®B = (AC®D, CE®A, A®B, CD®A, CB®D, AE®T, CE®D)

(CD)⁺=CDAB => B (CD)⁺=> CD→B (G - CD→B)⁺

Т.о. данная зависимость принадлежит замыканию (G - CD®B)+, т.е.

данная зависимость убирается из G:

G= (AC®D, CE®A, A®B, CD®A, CB®D, AE®T, CE®D)

b) AC®D:

G - AC®D = (CE®A, A®B, CD®A, CB®D, AE®T, CE®D)

(AC)⁺=ACBD => D (AC)⁺=> AC®D (G - AC®D)⁺

Т.о. данная зависимость принадлежит замыканию (G - AC®D)+, т.е.

данная зависимость убирается из G:

G= (CE®A, A®B, CD®A, CB®D, AE®T, CE®D)

c) CE®A:

G - CE®A = (A®B, CD®A, CB®D, AE®T, CE®D)

(CE)⁺=CEDATB => A (CE)⁺=> CE®A (G - CE®A)⁺

Т.о. данная зависимость принадлежит замыканию (G - CE®A)+, т.е.

данная зависимость убирается из G:

G= (A®B, CD®A, CB®D, AE®T, CE®D)

d) A®B:

G - A®B = (CD®A, CB®D, AE®T, CE®D)

(A)⁺=A => B Ï (A)⁺ => A®B Ï (G - A®B)

Т.о. данная зависимость не принадлежит замыканию (G- A®B)+, т.е. данная зависимость остается в G:

G= (A®B, CD®A, CB®D, AE®T, CE®D)

e) CD®A:

G - CD®A = (A®B, CB®D, AE®T, CE®D)

(CD)⁺=CD => A (CD)⁺=> CD®A (G - CD®A)⁺

Т.о. данная зависимость не принадлежит замыканию (G- CD®A)+, т.е. данная зависимость остается в G:

G= (A®B, CD®A, CB®D, AE®T, CE®D)

f) CB®D:

G - CB®D = (A®B, CD®A, AE®T, CE®D)

(CB)⁺=CB => D (CB)⁺=> CB®D (G - CB®D)⁺

Т.о. данная зависимость не принадлежит замыканию (G- CB®D)+, т.е. данная зависимость остается в G:

G= (A®B, CD®A, CB®D, AE®T, CE®D)

g) AE®T:

G - AE®T = (A®B, CD®A, CB®D, CE®D)

(AE)⁺=AEB => T (AE)⁺=> AE®T (G - AE®T)⁺

Т.о. данная зависимость не принадлежит замыканию (G - AE®T)+, т.е. данная зависимость остается в G:

G= (A®B, CD®A, CB®D, AE®T, CE®D)

h) CE®D:

G - CE®D = (A®B, CD®A, CB®D, AE®T)

(CE)⁺= CE => D (CE)⁺=> CE®D (G - CE®D)⁺

Т.о. данная зависимость не принадлежит замыканию (G - CE®D)+, т.е. данная зависимость остается в G:

G= (A®B, CD®A, CB®D, AE®T, CE®D)

В дальнейшем замыкание атрибутов рассматривается для полученного G.

Б. Проверяем принадлежность Z®A замыканию G, где Z Ì X:

a) A®B:

Данную функциональную зависимость рассматривать не будем, так как у неё в обеих частях только по одному атрибуту.

b) CD®A:

Рассмотрим следующие две зависимости:

C®A:

(C)⁺= C => A (C)⁺=> C®A (G)⁺. Следовательно, зависимость не заменяется

D®A:

(D)⁺= D => A (D)⁺=> D®A (G)⁺. Следовательно, зависимость не заменяется

c) CB®D:

Рассмотрим следующие две зависимости:

C®D:

(C)⁺= C => D (C)⁺=> C®D (G)⁺. Следовательно, зависимость не заменяется

B®D:

(B)⁺= B => D (B)⁺=> B®D (G)⁺. Следовательно, зависимость не заменяется

d) AE®T:

Рассмотрим следующие две зависимости:

A®T:

(A)⁺= AB => T (A)⁺=> A®T (G)⁺. Следовательно, зависимость не заменяется

E®T:

(E)⁺= E => T (E)⁺=> E®T (G)⁺. Следовательно, зависимость не заменяется

e) CE®D:

Рассмотрим следующие две зависимости:

C®D:

(C)⁺= C => D (C)⁺=> C®D (G)⁺. Следовательно, зависимость не заменяется

E®D:

(E)⁺= E => D (E)⁺=> E®D (G)⁺. Следовательно, зависимость не заменяется

Таким образом, G остается без изменений:

G= (A®B, CD®A, CB®D, AE®T, CE®D)

3) Данный шаг не выполняется, так как в G нет зависимостей с одинаковой левой частью.

Итак, минимальное покрытие G для F:

G= (A®B, CD®A, CB®D, AE®T, CE®D)

3. Получим множество схем отношений Q, заменив каждую зависимость V®W из G на VW:

Q=(AB, CDA, CBD, AET, CED)

4. Так как ABCDET Q, оставляем r без изменений и продолжаем выполнение алгоритма.

5. В Q вошли все атрибуты, следовательно r остается без изменений.

6. Добавляем в r все схемы отношений из Q:

r =(AB,CDA,CBD,AET,CED).

7. Определяем ключ для R:

1) i:=0, x₀=ABCDET;

2) (BCDET)⁺=BCDETA=R => x₁= BCDET, i:=1;

3) i возросло;

4) (CDET)⁺=CDETAB=R => x₂= CDET, i:=2;

5) i возросло;

6) (DET)⁺=DETR;

(CET)⁺=CETDAB=R => x₃= CDE, i:=3;

7) i возросло;

8) (ET)⁺=ETR;

(CT)⁺=CTR;

(CE)⁺=CEDATBR => x₄= CE, i:=4;

9) i возросло;

10) (C)⁺=CR;

(E)⁺=ER;

11) i не возросло. Следовательно, x₄= CE – ключ схемы отношений R.

Так как ключ найден, то в качестве новой схемы отношений добавлять в r какой-либо ключ для R не требуется.

Итак, получаем, что r =(AB,CDA,CBD,AET,CED) – «хорошая» схема БД.

Подставляя исходные данные, получим пять таблиц искомой БД:

1. {читаемый курс, преподаватель}

2. {час начала занятия, аудитория, читаемый курс}

3. {час начала занятия, преподаватель, аудитория}

4. {читаемый курс, студент, оценка по курсу}

5. {час начала занятия, студент, аудитория}

Ответ:

r =(AB,CDA,CBD,AET,CED) – «хорошая» схема БД.

2. Задача 2.

2.1. Постановка задачи.

Пусть задана грамматика арифметического выражения:

<F>::=(<E>) | i

Здесь: +,-,*,/,(,) – операторы,

i- константа или идентификатор,

<Z>,<E>,<T>,<F>- нетерминальные символы.

Задача:

Разработать спецификацию программы восходящего распознавателя для грамматики арифметического выражения. На вход распознавателя подается строка с предложением грамматики. На выходе должны получить результат арифметического выражения. Для описания использовать FlowForm или структурированный естественный язык.

2.2. Решение задачи.

Прежде чем разрабатывать спецификацию программы распознавателя необходимо определить отношения между операторами. Сведем эти отношения в таблицу:

r\s	+	-	*	/	(	)	\0
+	◦>	◦>	◦<	◦<	◦<	◦>	◦>
-	◦>	◦>	◦<	◦<	◦<	◦>	◦>
*	◦>	◦>	◦>	◦>	◦<	◦>	◦>
/	◦>	◦>	◦>	◦>	◦<	◦>	◦>
(	◦<	◦<	◦<	◦<	◦<	◦=	ошибка
)	◦>	◦>	◦>	◦>	ошибка	◦>	◦>

На основании таблицы отношений между операторами можно ввести следующие функции предшествования:

функция	+	-	*	/	(	)	\0
f	3	3	5	5	1	5	-
g	2	2	4	4	6	1	0

Теперь напишем на структурированном естественном языке спецификацию программы восходящего распознавателя в соответствии с алгоритмом входящего распознавателя для любой операторной грамматики.

Спецификация программы восходящего распознавателя:

@Вход – строка с предложением грамматик

@Выход – результат арифметического выражения

@НАЧАЛО Спецификации программы восходящего распознавателя

Создать стек Стек1;

Создать стек Стек2

Создать символы S1, S2;

Создать число Итог;

1: считать символ строки и записать в S2;

ЕСЛИ S2≠’+’ И S2≠’-’ И S2≠’*’ И S2≠’/’ И S2≠’(’ И S2≠’)’ И S2≠’\0’, ТО

поместить S2 в Стек2;

перейти к метке 1;

КОНЕЦ ЕСЛИ

2: ЕСЛИ S2=’+’ ИЛИ S2=’-’ ИЛИ S2=’*’ ИЛИ S2=’/’ ИЛИ S2=’(’ ИЛИ S2=’)’ ИЛИ S2=’\0’, ТО

считать последний из Стек1 в S1;

ЕСЛИ f(S1)<g(S2), ТО

Поместить S2 в s Стек1;

Перейти к метке 1;

КОНЕЦ ЕСЛИ

ЕСЛИ f(S1)>g(S2), ТО

вызвать программу обработки S1;

присвоить Итог результат операции S1

удалить S1 из Стек1;

удалить 2 последних элемента из Стек2;

поместить Итог в Стек2;

ЕСЛИ S1 = ‘/0’ и Стек1 пуст, ТО

перейти к метке 3

КОНЕЦ ЕСЛИ

перейти к метке 2;

КОНЕЦ ЕСЛИ

ЕСЛИ f(S1)=g(S2), ТО

удалить S1 из Стек1;

перейти к метке 1;

КОНЕЦ ЕСЛИ

3: считать Стек2 в Итог;

Выйти с результатом Итог;

@КОНЕЦ Спецификации программы восходящего распознавателя

3. Задача 3.

3.1. Постановка задачи.

Пусть задана схема БД ρ = (S, P, J, SPJ)

В схеме содержатся следующие таблицы, имеющие указанные поля:

S – Поставщик;

S = (номер_поставщика, имя, состояние, город)

P – Деталь;

P = (номер_детали, название, цвет, вес, город)

J – Изделие;

J = (номер_изделия, название, город)

SPJ – Сборка;

SPJ = (номер_поставщика, номер_детали, номер_изделия, количество деталей)

Задача:

Написать следующие запросы SQL:

1. Выдать номера изделий и названия городов, где они изготавливаются, такие, что второй буквой названия города является буква ‘а’.

2. Выдать номера деталей, поставляемых для какого-либо изделия поставщиком, проживающим в том же городе, где изготавливается это изделие.

3. Выдать номера поставщиков, поставляющих детали с номером ‘P1’ для какого-либо изделия в количестве большим, чем средний объем поставок детали с номером ‘P1’ для этого изделия.

4. Выдать номера изделий, для которых детали поставляет только поставщик с номером ‘S1’.

3.2. Решение задачи.

1. SELECT номер_изделия, город

FROM J

WHERE город LIKE ‘_а%’;

2. SELECT DISTINCT номер_детали

FROM SPJ

WHERE EXISTS

(SELECT *

FROM S,J

WHERE номер_поставщика = SPJ.номер_поставщика AND

номер_изделия = SPJ.номер_изделия AND

J.город = S.город);

3. SELECT DISTINCT номер_поставщика

FROM SPJ SX

WHERE номер_детали = ‘P1’ AND

количество>(SELECT AVG(количество)

FROM SPJ

WHERE номер_изделия = SX.номер_изделия AND

номер_детали = ‘P1’);

4. SELECT DISTINCT номер_изделия

FROM SPJ SX

WHERE NOT EXISTS

(SELECT *

FROM SPJ

WHERE номер_изделия = SX.номер_изделия AND

номер_поставщика != ‘S1’ );

4. Задача 4.

4.1. Постановка задачи.

Пусть на сервер базы данных поступает оператор SELECT, соответствующий следующему запросу:

"Выдать имена поставщиков из Лондона, которые поставляют для изделия с номером 'J1', по крайней мере, одну красную деталь".

Задача:

I. Написать соответствующий оператор SELECT и построить логический план выполнения этого оператора.

II. Определить оптимальный физический план выполнения оператора SELECT при следующих исходных данных.

1. Количество записей в таблицах:

T(S)=10000, T(P)=100000, T(SPJ)=1000000 .

2. Количество записей в одном блоке таблицы:

L_S=500, L_P=500, L_SPJ=1000_; L_join=2000 .

3. Индексы по атрибутам и число записей таблицы в одном блоке индекса (L):

- таблица S – 1) индекс по атрибуту "номер поставщика", L=200 ;

- таблица Р – 1) индекс по атрибуту "номер детали", L=200 ;

- таблица SPJ – 1) индекс по атрибуту "номер поставщика", L=200 ;

2) индекс по атрибуту "номер детали", L=200 ;

3) индекс по атрибуту "номер изделия", L=200 .

Примечания:

- записи таблиц могут читаться в отсортированном виде по своим индексированным атрибутам;

- записи во всех таблицах не сгруппированы (нет кластеризации).

4. Мощности атрибутов:

I(S, город) = 50, I(S, номер поставщика) = 10000,

I(Р, цвет) = 20, I(Р, номер детали)= 100000,

I(SPJ, номер поставщика)=5000, I(SPJ, номер детали)= 100000, I(SPJ, номер изделия)= 10000 .

5. Число блоков b=10, значения C_comp=C_move=C_fiiter=0.01мс, C_B=10 мс.

6. Предполагается, что используются левосторонние деревья для поиска оптимального плана и применяются каналы.

Примечание: метод хешированного соединения не рассматривать.

4.2. Решение задачи.

I. Оператор SELECT и логический план выполнения этого оператора.

Напишем оператор SELECT, соответствующий

SELECT DISTINCT имя

FROM S, SPJ, P

WHERE S.номер_поставщика=SPJ.номер_поставщика AND

SPJ.номер_детали=P.номер_детали AND

S.город=‘Лондон’ AND

SPJ.номер_изделия=‘J1’ AND

P.цвет=‘красный’;

Преобразуем запрос в формулу реляционной алгебры и оптимизируем её.

Введем условные обозначения:

R1 – таблица S;

R2 – таблица P;

R3 – таблица SPJ.

Преобразования в ходе оптимизации формулы будут проводиться с использованием законов реляционной алгебры:

3	Закон каскада проекции
4	Закон каскада селекции
5	Закон перестановки проекции и селекции
6	Закон перестановки селекции и декартова произведения
9	Закон перестановки проекции и декартова произведения

Нумерация законов соответствует нумерации, введенной в лекционных материалах.

Итак, оптимизированная формула, соответствующая составленному выше запросу:

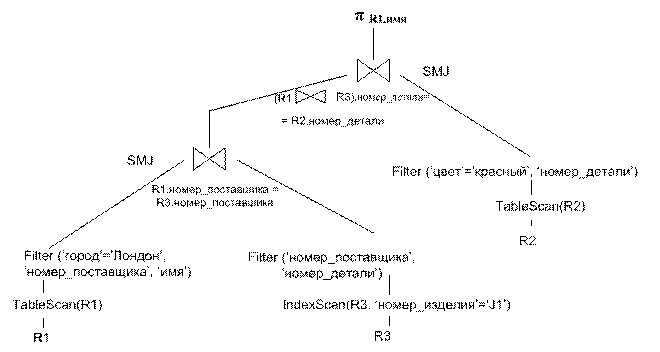
По этой формуле можно построить логический план выполнения запроса в графическом виде:

II. Физический план.

Построим физический план выполнения запроса.

Определим методы выбора записей.

1. Таблица R1.

Ø Чтение всей таблицы (j=1)

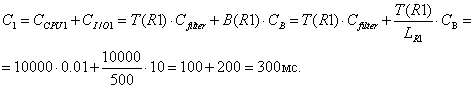
Ø Чтение записей с помощью индекса и их фильтрация (j=2)

По атрибуту «город» индекса нет

C = C₁ = 300мс.

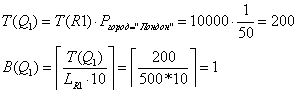
Ø Заполнение структуры str[1].

Str[1] = {{Q₁}, 0, 0, 300, 200, {200, 1, {200}, 1}}

2. Таблица R2

Ø Чтение всей таблицы (j=1)

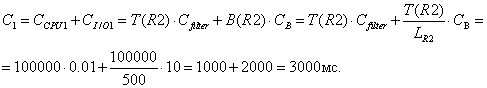
Ø Чтение записей с помощью индекса и их фильтрация (j=2)

По атрибуту «цвет» индекса нет.

C = C₁ = 3000мс.

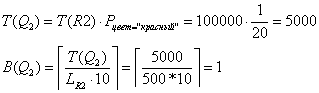
Ø Заполнение экземпляра структуры Str[2]:

Str[2] = {{Q₂}, 0, 0, 3000, 2000, {5000, 1, {5000}, 1}}

3. Таблица R3

Ø Чтение всей таблицы (j=1)

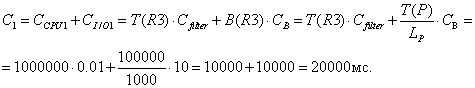
Ø Чтение записей с помощью индекса и их фильтрация (j=2)

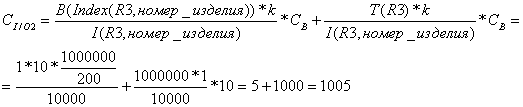
С₂ = + = 1+1005 = 1006

C = min{ C_1,C₂}= 1006 мс.

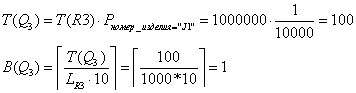
Ø Заполнение экземпляра структуры Str[3]:

Str[3] = {{Q₃}, 0, 0, 1006, 1005, {100, 1, {100, 100}, 2}}.

Определим методы соединения промежуточных таблиц.

не рассматриваем, так как эти таблицы не имеют пересечения по общему атрибуту.

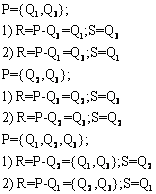
1. Рассмотрим соединение Q₁ и Q₃ по атрибуту «номер_поставщика».

Ø i=1 – метод соединения NLJ

мс

Ø i=2 - метод соединения SMJ

Обе таблицы отсортированы по атрибуту соединения.

мс //SMJ

мс

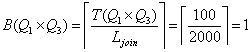
2. Рассмотрим соединение Q₃ и Q₁по атрибуту «номер_поставщика»_.

Ø i=1 – метод соединения NLJ

мс

Ø i=2 - метод соединения SMJ

Обе таблицы отсортированы по атрибуту соединения.

мс

Значения для соединения Q1xQ3 совпадают со значениями для соединения Q3xQ1, поэтому будем рассматривать только соединение Q1xQ3.

Заполняем запись str[4]

3. Рассматриваем соединение Q2xQ3 по атрибуту соединения «номер_детали».

Ø i=1 – метод соединения NLJ

мс

Ø i=2 - метод соединения SMJ

Обе таблицы отсортированы по атрибуту соединения.

мс

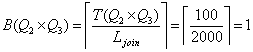
4. Рассматриваем соединение Q3xQ2 по атрибуту соединения «номер_детали».

Ø i=1 – метод соединения NLJ

мс

Ø i=2 - метод соединения SMJ

Обе таблицы отсортированы по атрибуту соединения.

мс

Значения для соединения Q2xQ3 совпадают со значениями для соединения Q3xQ2, поэтому будем рассматривать только соединение Q2xQ3.

Заполняем запись str[5].

5. Рассматриваем соединение (Q1xQ3)xQ2 по атрибуту соединения «номер_детали»

Ø i=1 – метод соединения NLJ

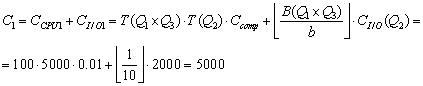
Ø i=2 - метод соединения SMJ

Только таблица Q2 отсортирована по атрибуту соединения.

мс

мс.

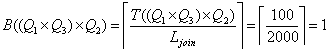
Заполняем запись str[6]

6. Рассматриваем соединение (Q2xQ3)xQ1 по атрибуту соединения «номер_поставщика».

Ø i=1 – метод соединения NLJ

мс

Ø i=2 - метод соединения SMJ

Только таблица Q1 отсортирована по атрибуту соединения.

мс

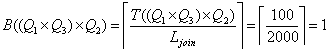
Значения для соединения (Q1xQ3)xQ2 совпадают со значениями для соединения (Q2xQ3)xQ1, поэтому рассматриваем только соединение (Q1xQ3)xQ2.

Таким образом, мы получили следующие варианты соединения, идентичные по стоимости:

1. (Q1xQ3)xQ2,

2. (Q3xQ1)xQ2,

3. (Q2xQ3)xQ1,

4. (Q3xQ2)xQ1.

Их стоимость составляет 4374.3 мс. Чтение таблиц R1, R2 производится полностью, чтение таблицы R3 производится по индексу (атрибут «номер изделия»).

Соединения таблиц производятся по методу SMJ.

Результат выбираем из экземпляра структуры str[6].

Оптимальный физический план представлен графически на следующем рисунке: